题目内容
8.化简求值:(x-2+$\frac{3}{x+2}$)÷$\frac{{x}^{2}+2x+1}{x+2}$,其中x=$\sqrt{2}$-1.分析 首先将括号里面通分运算,进而利用分式乘除运算法则计算得出答案.
解答 解:(x-2+$\frac{3}{x+2}$)÷$\frac{{x}^{2}+2x+1}{x+2}$,
=[$\frac{(x+2)(x-2)}{x+2}$+$\frac{3}{x+2}$]×$\frac{x+2}{(x+1)^{2}}$
=$\frac{{x}^{2}-1}{x+2}$×$\frac{x+2}{(x+1)^{2}}$
=$\frac{(x+1)(x-1)}{x+2}$×$\frac{x+2}{(x+1)^{2}}$
=$\frac{x-1}{x+1}$
把x=$\sqrt{2}$-1代入上式可得:
原式=$\frac{\sqrt{2}-2}{\sqrt{2}}$=1-$\sqrt{2}$.
点评 此题主要考查了分式的化简求值,正确掌握运算法则是解题关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
16. 如图,沿对角线AC折叠正方形ABCD,使得B、D重合,再折叠△ACD,点D恰好落在AC上的点E处,测得折痕AF的长为3,则C到AF的距离CG为( )
如图,沿对角线AC折叠正方形ABCD,使得B、D重合,再折叠△ACD,点D恰好落在AC上的点E处,测得折痕AF的长为3,则C到AF的距离CG为( )
 如图,沿对角线AC折叠正方形ABCD,使得B、D重合,再折叠△ACD,点D恰好落在AC上的点E处,测得折痕AF的长为3,则C到AF的距离CG为( )
如图,沿对角线AC折叠正方形ABCD,使得B、D重合,再折叠△ACD,点D恰好落在AC上的点E处,测得折痕AF的长为3,则C到AF的距离CG为( )| A. | $\frac{3}{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$-1 |
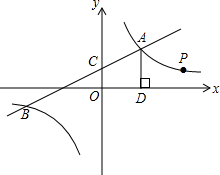 如图,一次函数y1=k1x+4与反比例函数y2=$\frac{{k}_{2}}{x}$的图象交于点A(2,m)和B(-6,-2)与y轴交于点C.
如图,一次函数y1=k1x+4与反比例函数y2=$\frac{{k}_{2}}{x}$的图象交于点A(2,m)和B(-6,-2)与y轴交于点C.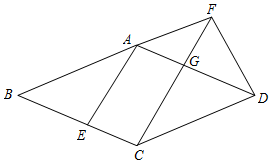 已知:如图,在菱形ABCD中,点E在边BC上,点F在BA的延长线上,BE=AF,CF∥AE,CF与边AD相交于点G.
已知:如图,在菱形ABCD中,点E在边BC上,点F在BA的延长线上,BE=AF,CF∥AE,CF与边AD相交于点G.