题目内容
4.解不等式组$\left\{\begin{array}{l}{\frac{x+3}{2}≥x+1}\\{3+4(x-1)>-9}\end{array}\right.$,并把解集在数轴上表示出来.
分析 分别求出各不等式的解集,再求出其公共解集,并把解集在数轴上表示出来即可.
解答 解:$\left\{\begin{array}{l}{\frac{x+3}{2}≥x+1①}\\{3+4(x-1)>-9②}\end{array}\right.$,
由①得x≤1,
由②得x>-2,
故不等式组的就为-2<x≤1.
把解集在数轴上表示出来为:
点评 此题考查的是解一元一次方程组的方法,解一元一次方程组应遵循的法则:“同大取较大,同小取较小,小大大小中间找,大大小小解不了”的原则.同时考查了在数轴上表示不等式的解集.

练习册系列答案
相关题目
9.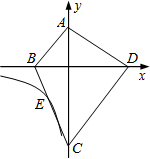 如图,四边形ABCD的顶点都在坐标轴上,若AB∥CD,△ABD与△ACD的面积分别为20和30,若双曲线y=$\frac{k}{x}$恰好经过BC的中点E,则k的值为( )
如图,四边形ABCD的顶点都在坐标轴上,若AB∥CD,△ABD与△ACD的面积分别为20和30,若双曲线y=$\frac{k}{x}$恰好经过BC的中点E,则k的值为( )
 如图,四边形ABCD的顶点都在坐标轴上,若AB∥CD,△ABD与△ACD的面积分别为20和30,若双曲线y=$\frac{k}{x}$恰好经过BC的中点E,则k的值为( )
如图,四边形ABCD的顶点都在坐标轴上,若AB∥CD,△ABD与△ACD的面积分别为20和30,若双曲线y=$\frac{k}{x}$恰好经过BC的中点E,则k的值为( )| A. | 3 | B. | -3 | C. | -6 | D. | 6 |
16. 如图,沿对角线AC折叠正方形ABCD,使得B、D重合,再折叠△ACD,点D恰好落在AC上的点E处,测得折痕AF的长为3,则C到AF的距离CG为( )
如图,沿对角线AC折叠正方形ABCD,使得B、D重合,再折叠△ACD,点D恰好落在AC上的点E处,测得折痕AF的长为3,则C到AF的距离CG为( )
 如图,沿对角线AC折叠正方形ABCD,使得B、D重合,再折叠△ACD,点D恰好落在AC上的点E处,测得折痕AF的长为3,则C到AF的距离CG为( )
如图,沿对角线AC折叠正方形ABCD,使得B、D重合,再折叠△ACD,点D恰好落在AC上的点E处,测得折痕AF的长为3,则C到AF的距离CG为( )| A. | $\frac{3}{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$-1 |
 观察如图所示的数阵,用A(m,n)表示第m行的第n个数,则依次规律A(5,3)为$\frac{13}{15}$.
观察如图所示的数阵,用A(m,n)表示第m行的第n个数,则依次规律A(5,3)为$\frac{13}{15}$.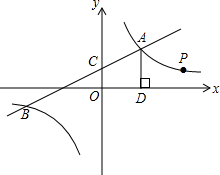 如图,一次函数y1=k1x+4与反比例函数y2=$\frac{{k}_{2}}{x}$的图象交于点A(2,m)和B(-6,-2)与y轴交于点C.
如图,一次函数y1=k1x+4与反比例函数y2=$\frac{{k}_{2}}{x}$的图象交于点A(2,m)和B(-6,-2)与y轴交于点C. 如图,在△ABC中,AB=AC=BC=8,点D为AB中点,点P从B点沿射线BC以2个单位/每秒运动,点Q从点C沿线段CA以1个单位/每秒运动,运动时间为t秒.求:
如图,在△ABC中,AB=AC=BC=8,点D为AB中点,点P从B点沿射线BC以2个单位/每秒运动,点Q从点C沿线段CA以1个单位/每秒运动,运动时间为t秒.求: