题目内容
19.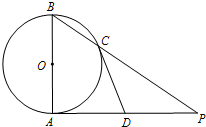 已知AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C,点D为AP的中点.求证:直线CD是⊙O的切线.
已知AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C,点D为AP的中点.求证:直线CD是⊙O的切线.
分析 连接OC,证出OC⊥CD即可.首先连接AC,得出直角三角形ACP,根据直角三角形斜边上中线等于斜边一半得CD=AD,再利用等腰三角形性质可证∠OCD=∠OAD=90°,从而解决问题.
解答  解:如图,连接OC、AC.
解:如图,连接OC、AC.
∵AB是⊙O的直径,
∴∠BCA=90°,
又∵∠ACP=180°-∠BCA=90°.
在Rt△APC中,D为AP的中点,
∴CD=$\frac{1}{2}$AP=AD.
∴∠4=∠3.
又∵OC=OA,
∴∠1=∠2.
∵∠2+∠4=∠PAB=90°,
∴∠1+∠3=∠2+∠4=90°.
即OC⊥CD.
∴直线CD是⊙O的切线.
点评 本题综合考查了圆周角定理、切线的判定与性质.正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
15. 如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若矩形的面积为16$\sqrt{3}$,AE=B′D,∠EFB=60°,则线段DE的长是( )
如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若矩形的面积为16$\sqrt{3}$,AE=B′D,∠EFB=60°,则线段DE的长是( )
 如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若矩形的面积为16$\sqrt{3}$,AE=B′D,∠EFB=60°,则线段DE的长是( )
如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若矩形的面积为16$\sqrt{3}$,AE=B′D,∠EFB=60°,则线段DE的长是( )| A. | 4$\sqrt{3}$ | B. | 5 | C. | 6 | D. | 6$\sqrt{3}$ |
7.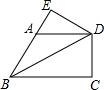 如图,在四边形ABCD中,∠ABC=60°,∠BAD=120°,∠ADC=90°,对角线BD平分∠ABC,过点D作DE⊥BA,交BA的延长线于点E.若AD=2,则四边形BCDE的周长为( )
如图,在四边形ABCD中,∠ABC=60°,∠BAD=120°,∠ADC=90°,对角线BD平分∠ABC,过点D作DE⊥BA,交BA的延长线于点E.若AD=2,则四边形BCDE的周长为( )
 如图,在四边形ABCD中,∠ABC=60°,∠BAD=120°,∠ADC=90°,对角线BD平分∠ABC,过点D作DE⊥BA,交BA的延长线于点E.若AD=2,则四边形BCDE的周长为( )
如图,在四边形ABCD中,∠ABC=60°,∠BAD=120°,∠ADC=90°,对角线BD平分∠ABC,过点D作DE⊥BA,交BA的延长线于点E.若AD=2,则四边形BCDE的周长为( )| A. | 6+$\sqrt{3}$ | B. | 6+2$\sqrt{3}$ | C. | 7+$\sqrt{3}$ | D. | 7+2$\sqrt{3}$ |
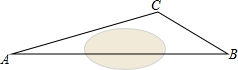 在一次课外实践活动中,同学们要测量某公园人工湖两侧A,B两个凉亭之间的距离.如图,现测得∠ABC=30°,∠CAB=15°,AC=200米,请计算A,B两个凉亭之间的距离(结果精确到1米)(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
在一次课外实践活动中,同学们要测量某公园人工湖两侧A,B两个凉亭之间的距离.如图,现测得∠ABC=30°,∠CAB=15°,AC=200米,请计算A,B两个凉亭之间的距离(结果精确到1米)(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
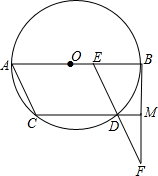 已知:如图,点E是⊙O的直径,AB上一个动点(与A,B不重合),在AB下方有一条弦CD始终与AB保持平行,且AE=CD.连接AC,ED,延长ED交⊙O切线BF于点F,延长CD交BF于点M.请探究当点E在运动时:
已知:如图,点E是⊙O的直径,AB上一个动点(与A,B不重合),在AB下方有一条弦CD始终与AB保持平行,且AE=CD.连接AC,ED,延长ED交⊙O切线BF于点F,延长CD交BF于点M.请探究当点E在运动时: