题目内容
8.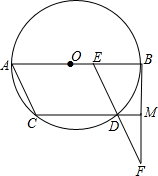 已知:如图,点E是⊙O的直径,AB上一个动点(与A,B不重合),在AB下方有一条弦CD始终与AB保持平行,且AE=CD.连接AC,ED,延长ED交⊙O切线BF于点F,延长CD交BF于点M.请探究当点E在运动时:
已知:如图,点E是⊙O的直径,AB上一个动点(与A,B不重合),在AB下方有一条弦CD始终与AB保持平行,且AE=CD.连接AC,ED,延长ED交⊙O切线BF于点F,延长CD交BF于点M.请探究当点E在运动时:(1)四边形ACDE能够成为菱形吗?写出你的猜想并给予证明.
(2)MB与MF数量关系是否发生变化?写出猜想并给予证明.
分析 (1)由条件可证明四边形ACDE为平行四边形,当E点运动到O点时,则有AE=ED,四边形ACDE为菱形;
(2)由条件可证明AC=BD=DE,再利用切线的性质可证得BD=DF,可证明D为EF的中点,则M为BF的中点,可得出结论.
解答 解:
(1)当点E运动到与点O重合时,四边形ACDE为菱形.
证明如下:
∵AE∥CD,且AE=CD,
∴四边形ACDE为平行四边形,
当点E与点O重合时,EA=ED,
∴四边形ACDE为菱形;
(2)不发生变化,证明如下:
如图,连接AD、BD,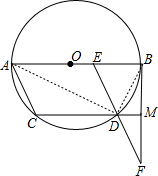
∵AB∥CD,
∴∠ADC=∠DAB,
∴$\widehat{AC}$=$\widehat{BD}$,
∴AC=BD,
在平行四边形ACDE中,ED=AC,
∴DE=BD,
∴∠DEB=∠DBE,
∵BF与⊙O相切,
∴∠EBF=90°,
∴∠DEB+∠F=∠DBE+∠DBF=90°,
∴∠DBF=∠F,
∴DB=DF,
∴DE=DF,
∵DM∥EB,
∴MB=MF.
点评 本题为圆的综合应用,涉及知识点有菱形的判定和性质、切线的性质及三角形中位线定理的逆定理等.在(1)中注意利用好圆的半径相等,在(2)中证得D是EF的中点是解题的关键.本题考查知识点相对基础,难度不大.

练习册系列答案
相关题目
16.已知x为实数,且$\frac{3}{{x}^{2}+9x}-({x}^{2}+9x)=2$,那么x2+9x的值为( )
| A. | 1 | B. | -3或1 | C. | 3 | D. | -1或3 |
3.已知一个直角三角形的两条边长分别是6和8,则第三边长是( )
| A. | 10 | B. | 8 | C. | 2$\sqrt{7}$ | D. | 10或2$\sqrt{7}$ |
13. 如图,正方形ABCD的边长为2,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…按照此规律继续下去,则S2016的值为( )
如图,正方形ABCD的边长为2,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…按照此规律继续下去,则S2016的值为( )
 如图,正方形ABCD的边长为2,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…按照此规律继续下去,则S2016的值为( )
如图,正方形ABCD的边长为2,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…按照此规律继续下去,则S2016的值为( )| A. | ($\frac{\sqrt{2}}{2}$)2013 | B. | ($\frac{\sqrt{2}}{2}$)2014 | C. | ($\frac{1}{2}$)2013 | D. | ($\frac{1}{2}$)2014 |
20.一个等腰三角形的两条边长分别是方程x2-7x+10=0的两根,则这个等腰三角形的腰长是( )
| A. | 2 | B. | 5 | C. | 2或5 | D. | 3或4 |
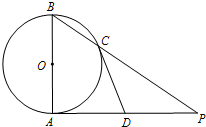 已知AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C,点D为AP的中点.求证:直线CD是⊙O的切线.
已知AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C,点D为AP的中点.求证:直线CD是⊙O的切线. 如图,在Rt△ABC中,AB=AC,∠BAC=90°,O为BC的中点.
如图,在Rt△ABC中,AB=AC,∠BAC=90°,O为BC的中点.