题目内容
14.将下列各多项式因式分解(1)15a2+5a
(2)x5-x3
(3)a3b-4a2b2+4ab3
(4)1-x2-y2+x2y2.
分析 (1)此多项式有公因式,应提取公因式5a,然后再整理即可.
(2)先提取公因式x3,再利用平方差公式继续进行因式分解.
(3)先提取公因式ab,再对余下的多项式利用完全平方公式继续分解.
(4)用分组分解法,前两项一组,后两项一组,提取公因式,两组之间提取提取公因式,再用平方差公式分解,即可.
解答 解:(1)原式=5a(3a+1);
(2)原式=x3(x2-1)=x3(x+1)(x-1);
(3)原式=ab(a2-4ab+4b2)=ab(a-2b)2.
(4)原式=(1-x2)-(y2-x2y2)=(1-x2)-y2(1-x2)=(1-x2)(1-y2)=(1+x)(1-x)(1+y)(1-y).
点评 本题考查了用提公因式法和公式法进行因式分解,一个多项式有公因式首先提取公因式,然后再用其他方法进行因式分解,同时因式分解要彻底,直到不能分解为止.(4)用分组分解法,分组是解本小题的难点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.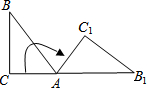 如图,在三角形ABC中,∠C=90°,∠B=35°,将三角形ABC绕点A按顺时针方向旋转到三角形AB1C1的位置,使得点C、A、B1在一条直线上,那么旋转角等于( )
如图,在三角形ABC中,∠C=90°,∠B=35°,将三角形ABC绕点A按顺时针方向旋转到三角形AB1C1的位置,使得点C、A、B1在一条直线上,那么旋转角等于( )
 如图,在三角形ABC中,∠C=90°,∠B=35°,将三角形ABC绕点A按顺时针方向旋转到三角形AB1C1的位置,使得点C、A、B1在一条直线上,那么旋转角等于( )
如图,在三角形ABC中,∠C=90°,∠B=35°,将三角形ABC绕点A按顺时针方向旋转到三角形AB1C1的位置,使得点C、A、B1在一条直线上,那么旋转角等于( )| A. | 145° | B. | 125° | C. | 70° | D. | 55° |
9. 如图,点A表示的实数是( )
如图,点A表示的实数是( )
 如图,点A表示的实数是( )
如图,点A表示的实数是( )| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | $-\sqrt{5}$ | D. | $-\sqrt{3}$ |
3.已知一个直角三角形的两条边长分别是6和8,则第三边长是( )
| A. | 10 | B. | 8 | C. | 2$\sqrt{7}$ | D. | 10或2$\sqrt{7}$ |
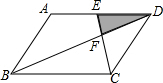 如图,平行四边形ABCD中,E为AD的中点,连结CE,与对角线BD交于点F,若平行四边形ABCD的面积为24cm2,则△DEF的面积为2cm2.
如图,平行四边形ABCD中,E为AD的中点,连结CE,与对角线BD交于点F,若平行四边形ABCD的面积为24cm2,则△DEF的面积为2cm2.
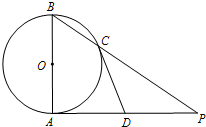 已知AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C,点D为AP的中点.求证:直线CD是⊙O的切线.
已知AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C,点D为AP的中点.求证:直线CD是⊙O的切线.