题目内容
7.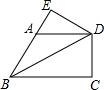 如图,在四边形ABCD中,∠ABC=60°,∠BAD=120°,∠ADC=90°,对角线BD平分∠ABC,过点D作DE⊥BA,交BA的延长线于点E.若AD=2,则四边形BCDE的周长为( )
如图,在四边形ABCD中,∠ABC=60°,∠BAD=120°,∠ADC=90°,对角线BD平分∠ABC,过点D作DE⊥BA,交BA的延长线于点E.若AD=2,则四边形BCDE的周长为( )| A. | 6+$\sqrt{3}$ | B. | 6+2$\sqrt{3}$ | C. | 7+$\sqrt{3}$ | D. | 7+2$\sqrt{3}$ |
分析 根据正弦的概念求出DE,根据余弦的概念求出AE,根据角平分线的性质得到DC=DE=$\sqrt{3}$,根据平行线的性质得到AB=AD,利用周长公式计算即可.
解答 解:∵∠BAD=120°,
∴∠EAD=60°,
∴DE=AD•sin∠EAD=$\sqrt{3}$,AE=1,
∵BD平分∠ABC,DE⊥BA,∠ADC=90°,
∴DC=DE=$\sqrt{3}$,
∵BD平分∠ABC,∠ABC=60°,
∴∠DBC=30°,
∴BC=$\frac{DC}{tan∠DBC}$=3,
∵∠ABC=60°,∠BAD=120°,
∴AD∥BC,
∴∠ADB=∠DBC,
∴∠ADB=∠ABD,
∴AB=AD=2,
∴BE=3,
∴四边形BCDE的周长为3+3+$\sqrt{3}$+$\sqrt{3}$=6+2$\sqrt{3}$,
故选:B.
点评 本题考查的是角平分线的性质、锐角三角函数的概念,掌握角的平分线上的点到角的两边的距离相等是解题的关键.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
16.已知x为实数,且$\frac{3}{{x}^{2}+9x}-({x}^{2}+9x)=2$,那么x2+9x的值为( )
| A. | 1 | B. | -3或1 | C. | 3 | D. | -1或3 |
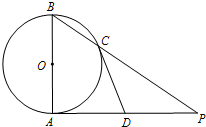 已知AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C,点D为AP的中点.求证:直线CD是⊙O的切线.
已知AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C,点D为AP的中点.求证:直线CD是⊙O的切线. 如图,在Rt△ABC中,AB=AC,∠BAC=90°,O为BC的中点.
如图,在Rt△ABC中,AB=AC,∠BAC=90°,O为BC的中点.