题目内容
15. 如图,已知长方体的长宽高分别为4、2、1,一只蚂蚁沿长方体的表面,从点A爬到点B,最短路程为( )
如图,已知长方体的长宽高分别为4、2、1,一只蚂蚁沿长方体的表面,从点A爬到点B,最短路程为( )| A. | $\sqrt{29}$ | B. | $\sqrt{37}$ | C. | $\sqrt{21}$ | D. | 5 |
分析 蚂蚁有三种爬法,就是把正视和俯视(或正视和侧视,或俯视和侧视)二个面展平成一个长方形,然后求其对角线,比较大小即可求得最短的途径.
解答 解:如图所示,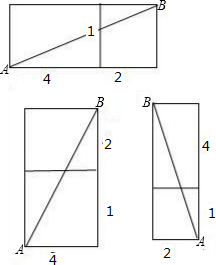
路径一:AB=$\sqrt{{6}^{2}+{1}^{2}}=\sqrt{37}$;
路径二:AB=$\sqrt{{4}^{2}+{3}^{2}}=5$;
路径三:AB=$\sqrt{{2}^{2}+{5}^{2}}=\sqrt{29}$;
∵37>29>25,
∴5cm为最短路径.
故选D.
点评 此题考查平面的最短路径问题,关键是把长方体拉平后用了勾股定理求出对角线的长度.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.在△ABC中,a:b:c=1:1:$\sqrt{2}$,那么△ABC是( )
| A. | 等腰三角形 | B. | 钝角三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
10. 如图,△ABC是⊙O的内接三角形,∠AOB=135°,则∠ACB的度数为( )
如图,△ABC是⊙O的内接三角形,∠AOB=135°,则∠ACB的度数为( )
 如图,△ABC是⊙O的内接三角形,∠AOB=135°,则∠ACB的度数为( )
如图,△ABC是⊙O的内接三角形,∠AOB=135°,则∠ACB的度数为( )| A. | 35° | B. | 55° | C. | 60° | D. | 67.5° |
9. 如图,已知AB∥CD,那么下列结论中正确的是( )
如图,已知AB∥CD,那么下列结论中正确的是( )
 如图,已知AB∥CD,那么下列结论中正确的是( )
如图,已知AB∥CD,那么下列结论中正确的是( )| A. | ∠3=∠4 | B. | ∠1=∠2 | C. | ∠2=∠3 | D. | ∠1+∠ACD=180° |
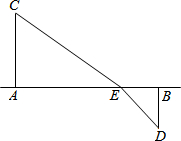 如图所示铁路上A、B两站(视为两个点)相距25km,C、D为两村庄(视为两个点),CA⊥AB于点A,DB⊥AB于点B,已知CA=15km,DB=10km.现要在A.B之间建一个土特产收购站E,当AE=xkm时
如图所示铁路上A、B两站(视为两个点)相距25km,C、D为两村庄(视为两个点),CA⊥AB于点A,DB⊥AB于点B,已知CA=15km,DB=10km.现要在A.B之间建一个土特产收购站E,当AE=xkm时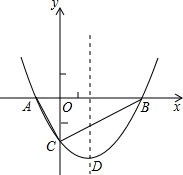 如图,抛物线y=$\frac{1}{2}$x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0).
如图,抛物线y=$\frac{1}{2}$x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0).