题目内容
3.已知抛物线C1:y=x2-2(m-1)x+m2-3m-1(1)证明:不论m为何值,抛物线图象的顶点M均在某一直线l的图象上,求此直线l的函数解析式;
(2)当m=2时,点P为抛物线上一点,且∠MOP=90°,求点P的坐标;
(3)将(2)中的抛物线C1沿x轴翻折再向上平移1个单位向右平移n个单位得抛物线C2,设抛物线C2的顶点为N,抛物线C2与x轴相交于点A,B(A在B的左边),且AM∥BN,求n的值.
分析 (1)利用配方法可确定抛物线的顶点M坐标为(m-1,-m-2),然后令x=m-1,y=-m-2,然后消去m得到x和y的关系式即可;
(2)先确定抛物线解析式为y=x2-2x-3,点M的坐标为(1,-4),利用旋转的定义,将线段OM绕点O逆时针旋转90°得线段OC,与抛物线相交于点P,如图1,从而得到点C坐标,再求出直线OP的解析式为y=$\frac{1}{4}$x,然后解方程组$\left\{\begin{array}{l}{y=\frac{1}{4}x}\\{y={x}^{2}-2x-3}\end{array}\right.$得P点坐标;
(3)利用抛物线的几何变换得到N(n+1,5),抛物线C2的解析式为y=-(x-n-1)2+5,过点M作ME⊥x轴于点E,过点N作NF⊥x轴于点F,如图2,根据抛物线与x轴的交点问题求出A点和B点坐标,然后证明Rt△AME∽Rt△BNF,再利用相似比得到关于n的方程,解方程可得到n的值.
解答 (1)证明:y=x2-2(m-1)x+m2-3m-1=[x-(m-1)]2-m-2,则抛物线的顶点M坐标为(m-1,-m-2),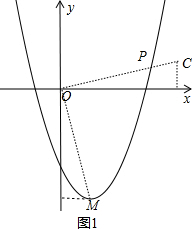
令x=m-1,y=-m-2,
则x+y=-3,
所以直线l的函数解析式为y=-x-3;
(2)解:当m=2时,抛物线解析式为y=x2-2x-3,点M的坐标为(1,-4),
将线段OM绕点O逆时针旋转90°得线段OC,与抛物线相交于点P,如图1,
则点C坐标为(4,1),设直线OC的解析式为y=kx,
把C(4,1)代入得4k=1,解得k=$\frac{1}{4}$,
所以直线OP的解析式为y=$\frac{1}{4}$x,
解方程组$\left\{\begin{array}{l}{y=\frac{1}{4}x}\\{y={x}^{2}-2x-3}\end{array}\right.$得$\left\{\begin{array}{l}{x=\frac{9+\sqrt{273}}{8}}\\{y=\frac{9+\sqrt{273}}{32}}\end{array}\right.$或$\left\{\begin{array}{l}{x=\frac{9-\sqrt{273}}{8}}\\{y=\frac{9-\sqrt{273}}{32}}\end{array}\right.$,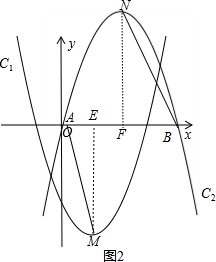
所以点P的坐标为($\frac{9+\sqrt{273}}{8}$,$\frac{9+\sqrt{273}}{32}$)或($\frac{9-\sqrt{273}}{8}$,$\frac{9-\sqrt{273}}{32}$);
(3)解:由题意可知,抛物线C2的顶点N(n+1,5),则抛物线C2的解析式为y=-(x-n-1)2+5,
过点M作ME⊥x轴于点E,过点N作NF⊥x轴于点F,如图2,
当y=0时,-(x-n-1)2+5=0,解得x1=n+1-$\sqrt{5}$,x2=n+1+$\sqrt{5}$,
∴A(n+1-$\sqrt{5}$,0),B(n+1+$\sqrt{5}$,0),
∵AM∥BN,
∴∠MAE=∠NBF,
∴Rt△AME∽Rt△BNF,
∴$\frac{ME}{NF}$=$\frac{AE}{BF}$,即$\frac{4}{5}$=$\frac{1-(n+1-\sqrt{5})}{n+1+\sqrt{5}-(n+1)}$,
∴n=$\frac{\sqrt{5}}{5}$.
点评 本题考查了二次函数的综合题:熟练掌握二次函数的性质和抛物线的几何变换;会求抛物线与直线的交点坐标、抛物线与x轴的交点坐标;利用旋转确定OP的直线解析式是解决(2)小题的关键;利用几何变换画出图象和利用相似比建立等量关系是解决(3)小题的关键.

 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案| A. | 18 | B. | 12 | C. | 11 | D. | 8 |
| A. | a>0 | B. | a>2 | C. | a<0 | D. | a<2 |
 如图,已知长方体的长宽高分别为4、2、1,一只蚂蚁沿长方体的表面,从点A爬到点B,最短路程为( )
如图,已知长方体的长宽高分别为4、2、1,一只蚂蚁沿长方体的表面,从点A爬到点B,最短路程为( )| A. | $\sqrt{29}$ | B. | $\sqrt{37}$ | C. | $\sqrt{21}$ | D. | 5 |
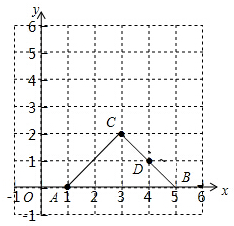 如图,点A、B、C、D的坐标分别是(1,0)、(5,0)、(3,2)、(4,1),如果以点C、D、E为顶点的直角三角形与△ABC相似,则E点的坐标可能是下列的( )
如图,点A、B、C、D的坐标分别是(1,0)、(5,0)、(3,2)、(4,1),如果以点C、D、E为顶点的直角三角形与△ABC相似,则E点的坐标可能是下列的( )①(2,1)②(3,1)③(4,2)④(5,2)
| A. | ①③ | B. | ②④ | C. | ①②③ | D. | ①②③④ |
①线段;②等边三角形;③矩形;④菱形;⑤五角星;⑥圆.
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
 如图,张萌的手中有一张正方形纸片ABCD(AD∥BC),点E,F分别在AB个CD上,且EF∥AD,此时张萌判断出EF∥BC,则张萌判断出该结论的理由是如果两条直线都和第三条直线平行,那么这两条直线也平行.
如图,张萌的手中有一张正方形纸片ABCD(AD∥BC),点E,F分别在AB个CD上,且EF∥AD,此时张萌判断出EF∥BC,则张萌判断出该结论的理由是如果两条直线都和第三条直线平行,那么这两条直线也平行.