题目内容
10.某数学兴趣小组在学习二次根式$\sqrt{{a}^{2}}$=|a|后,研究了如下四个问题,其中错误的是( )| A. | 在a>1的条件下化简代数式a+$\sqrt{{a}^{2}-2a+1}$的结果为2a-1 | |
| B. | a+$\sqrt{{a}^{2}-2a+1}$的值随a变化而变化,当a取某个数值时,上述代数式的值可以为$\frac{1}{2}$ | |
| C. | 当a+$\sqrt{{a}^{2}-2a+1}$的值恒为定值时,字母a的取值范围是a≤1 | |
| D. | 若$\sqrt{{a}^{2}-2a+1}$=($\sqrt{a-1}$)2,则字母a必须满足a≥1 |
分析 首先将原式变形为a+$\sqrt{(a-1)^{2}}$,然后再根据$\sqrt{{a}^{2}}$=|a|,将原式变形为a+|a-1|,然后依据绝对值的性质分类化简即可得出结论.
解答 解:A.原式=a+$\sqrt{(a-1)^{2}}$=a+|a-1|,当a>1时,原式=a+a-1=2a-1,故A不符合题意;
B.当a>1时,原式=2a-1>1;当a≤1时,原式=1,故B符合题意;
C.原式=a+$\sqrt{(a-1)^{2}}$=a+|a-1|,当a≤1时,原式=a+|a-1|=a+1-a=1,故C不符合题意;
D.由$\sqrt{{a}^{2}}$=($\sqrt{a}$)2(a≥0),故D不符合题意.
故选:B.
点评 本题主要考查的是$\sqrt{{a}^{2}}$化简和绝对值的性质,掌握$\sqrt{{a}^{2}}$=|a|以及绝对值的性质是解题的关键.

练习册系列答案
相关题目
18.某校九年级(1)班的10名同学在“献爱心,关注留守儿童”捐款活动中,捐款情况如下(单位:元)10,8,12,15,10,12,11,9,10,13.关于这组数据,下列说法正确的是( )
| A. | 众数是10.5 | B. | 中位数是10 | C. | 平均数是11 | D. | 以上说法均不对 |
5.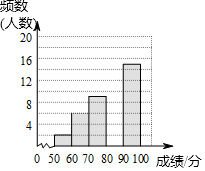 为了传承中华优秀传统文化,某校组织了一次九年级350名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中若干名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
为了传承中华优秀传统文化,某校组织了一次九年级350名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中若干名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
请根据所给信息,解答下列问题:
(1)b=0.18;
(2)请补全频数分布直方图;
(3)这次比赛成绩的中位数会落在80≤x<90分数段;
(4)若成绩在90分以上(包括90分)的为“优”等,则该年级参加这次比赛的350名学生中成绩“优”等的约有多少人?
 为了传承中华优秀传统文化,某校组织了一次九年级350名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中若干名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
为了传承中华优秀传统文化,某校组织了一次九年级350名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中若干名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:| 成绩x/分 | 频数 | 频率 |
| 50≤x<60 | 2 | 0.04 |
| 60≤x<70 | 6 | 0.12 |
| 70≤x<80 | 9 | b |
| 80≤x<90 | a | 0.36 |
| 90≤x<100 | 15 | 0.30 |
(1)b=0.18;
(2)请补全频数分布直方图;
(3)这次比赛成绩的中位数会落在80≤x<90分数段;
(4)若成绩在90分以上(包括90分)的为“优”等,则该年级参加这次比赛的350名学生中成绩“优”等的约有多少人?
20.不等式组$\left\{\begin{array}{l}{2x+3<1}\\{2(x-2)>3x}\end{array}\right.$的解集是( )
| A. | x<-2 | B. | x<-4 | C. | -4<x<-2 | D. | 无解 |
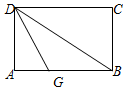 如图,将矩形纸片ABCD折叠,先折出折痕(对角线)BD,再折叠,使边DA与对角线BD重合,得折痕DG,若AB=8,BC=6,则AG的长是3.
如图,将矩形纸片ABCD折叠,先折出折痕(对角线)BD,再折叠,使边DA与对角线BD重合,得折痕DG,若AB=8,BC=6,则AG的长是3. 如图是我国古代某种铜钱的平面示意图,该图形是在一个圆形的中间挖去一个正方形得到的.若圆的半径是3cm,正方形的边长为xcm,设该图形的面积为ycm2.(注:π取3)
如图是我国古代某种铜钱的平面示意图,该图形是在一个圆形的中间挖去一个正方形得到的.若圆的半径是3cm,正方形的边长为xcm,设该图形的面积为ycm2.(注:π取3)