题目内容
15．分解因式（1）ax2-16ay2
（2）-2a3+12a2-18a
（3）a2（x-y）-4b2（x-y）
分析 （1）首先提出公因式a，再利用平方差公式进行二次分解即可；
（2）首先提出公因式-2a，再利用完全平方公式进行二次分解即可；
（3）首先提出公因式x-y，再利用平方差公式进行二次分解即可．
解答 解：（1）原式=a（x2-16y2）=a（x+4y）（x-4y）；
（2）原式=-2a（a2-6a+9）=-2a（a-3）2；
（3）原式=（x-y）（a2-4b2）=（x-y）（a+2b）（a-2b）．
点评 本题考查了提公因式法与公式法分解因式，要求灵活使用各种方法对多项式进行因式分解，一般来说，如果可以先提取公因式的要先提取公因式，再考虑运用公式法分解．
练习册系列答案
名校课堂系列答案
相关题目
10．某数学兴趣小组在学习二次根式$\sqrt{{a}^{2}}$=|a|后，研究了如下四个问题，其中错误的是（ ）
| A． | 在a＞1的条件下化简代数式a+$\sqrt{{a}^{2}-2a+1}$的结果为2a-1 | |
| B． | a+$\sqrt{{a}^{2}-2a+1}$的值随a变化而变化，当a取某个数值时，上述代数式的值可以为$\frac{1}{2}$ | |
| C． | 当a+$\sqrt{{a}^{2}-2a+1}$的值恒为定值时，字母a的取值范围是a≤1 | |
| D． | 若$\sqrt{{a}^{2}-2a+1}$=（$\sqrt{a-1}$）2，则字母a必须满足a≥1 |
7．下列命题是真命题的是（ ）
| A． | 同旁内角互补 | |
| B． | 三角形的一个外角等于两个内角的和 | |
| C． | 若a2=b2，则a=b | |
| D． | 同角的余角相等 |
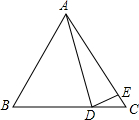如图，△ABC中，∠B=65°，∠BAD=40°，∠AED=100°，∠CDE=45°，求∠CAD的度数．