题目内容
18．某校九年级（1）班的10名同学在“献爱心，关注留守儿童”捐款活动中，捐款情况如下（单位：元）10，8，12，15，10，12，11，9，10，13．关于这组数据，下列说法正确的是（ ）| A． | 众数是10.5 | B． | 中位数是10 | C． | 平均数是11 | D． | 以上说法均不对 |
分析 根据平均数和中位数、众数的概念求解可得．
解答 解：以上数据重新排列为：8、9、10、10、10、11、12、12、13、15，
∴众数为10、中位数为$\frac{10+11}{2}$=10.5，平均数为（8+9+10+10+10+11+12+12+13+15）÷10=10，
故选：D．
点评 本题考查的是平均数、众数和中位数的概念；熟练掌握平均数和中位数、众数的概念是解题的关键．
练习册系列答案
相关题目
如图，已知线段AB=2，MN⊥AB于点M，且AM=BM，P是射线MN上一动点，E，D分别是PA，PB的中点，过点A，M，D的圆与BP的另一交点C（点C在线段BD上），连结AC，DE．
10．某数学兴趣小组在学习二次根式$\sqrt{{a}^{2}}$=|a|后，研究了如下四个问题，其中错误的是（ ）
| A． | 在a＞1的条件下化简代数式a+$\sqrt{{a}^{2}-2a+1}$的结果为2a-1 | |
| B． | a+$\sqrt{{a}^{2}-2a+1}$的值随a变化而变化，当a取某个数值时，上述代数式的值可以为$\frac{1}{2}$ | |
| C． | 当a+$\sqrt{{a}^{2}-2a+1}$的值恒为定值时，字母a的取值范围是a≤1 | |
| D． | 若$\sqrt{{a}^{2}-2a+1}$=（$\sqrt{a-1}$）2，则字母a必须满足a≥1 |
7．下列命题是真命题的是（ ）
| A． | 同旁内角互补 | |
| B． | 三角形的一个外角等于两个内角的和 | |
| C． | 若a2=b2，则a=b | |
| D． | 同角的余角相等 |
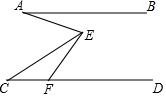如图，已知AB∥CD，F为CD上一点，∠EFD=60°，∠AEC=2∠CEF，若6°＜∠BAE＜15°，∠C的度数为整数，则∠C的度数为36°或37°．