题目内容
5.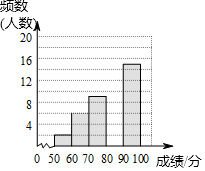 为了传承中华优秀传统文化,某校组织了一次九年级350名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中若干名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
为了传承中华优秀传统文化,某校组织了一次九年级350名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中若干名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:| 成绩x/分 | 频数 | 频率 |
| 50≤x<60 | 2 | 0.04 |
| 60≤x<70 | 6 | 0.12 |
| 70≤x<80 | 9 | b |
| 80≤x<90 | a | 0.36 |
| 90≤x<100 | 15 | 0.30 |
(1)b=0.18;
(2)请补全频数分布直方图;
(3)这次比赛成绩的中位数会落在80≤x<90分数段;
(4)若成绩在90分以上(包括90分)的为“优”等,则该年级参加这次比赛的350名学生中成绩“优”等的约有多少人?
分析 (1)根据频率之和1,即可解决问题;
(2)先求出总人数,再利用频率公式即可解决问题;
(3)根据中位数的定义即可判断;
(4)利用样本估计总体的思想即可解决问题;
解答 解:(1)b=1-0.04-0.12-0.36-0.30-=0.18.
故答案为0.18.
(2)总人数=6÷0.12=50,50×0.36=18,
条形图如图所示,
(3)这次比赛成绩的中位数落在80≤x<90之间.
故答案为80≤x<90.
(4)350×0.3=105人.
答:该年级参加这次比赛的350名学生中成绩“优”等的约有105人.
点评 本题考查频数分布直方图、频数分布表、中位数等知识,解题的关键是掌握基本概念,熟练应用所学知识解决问题.

练习册系列答案
相关题目
15.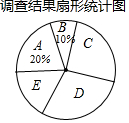 2017年全国两会民生话题成为社会焦点.徐州市记者为了了解百姓“两会民生话题”的聚焦点,随机调查了徐州市部分市民,并对调查结果进行整理.绘制了如图所示的不完整的统计图表.
2017年全国两会民生话题成为社会焦点.徐州市记者为了了解百姓“两会民生话题”的聚焦点,随机调查了徐州市部分市民,并对调查结果进行整理.绘制了如图所示的不完整的统计图表.
请根据图表中提供的信息解答下列问题:
(1)填空:m=40,n=100.扇形统计图中E组所占的百分比为15%;
(2)徐州市市区人口现有170万人,请你估计其中关注D组话题的市民人数;
(3)若在这次接受调查的市民中,随机抽查一人,则此人关注C组话题的概率是多少?
 2017年全国两会民生话题成为社会焦点.徐州市记者为了了解百姓“两会民生话题”的聚焦点,随机调查了徐州市部分市民,并对调查结果进行整理.绘制了如图所示的不完整的统计图表.
2017年全国两会民生话题成为社会焦点.徐州市记者为了了解百姓“两会民生话题”的聚焦点,随机调查了徐州市部分市民,并对调查结果进行整理.绘制了如图所示的不完整的统计图表.| 组别 | 焦点话题 | 频数(人数) |
| A | 食品安全 | 80 |
| B | 教育医疗 | m |
| C | 就业养老 | n |
| D | 生态环保 | 120 |
| E | 其他 | 60 |
(1)填空:m=40,n=100.扇形统计图中E组所占的百分比为15%;
(2)徐州市市区人口现有170万人,请你估计其中关注D组话题的市民人数;
(3)若在这次接受调查的市民中,随机抽查一人,则此人关注C组话题的概率是多少?
16.-5的倒数的相反数是( )
| A. | 5 | B. | $\frac{1}{5}$ | C. | -5 | D. | $-\frac{1}{5}$ |
10.某数学兴趣小组在学习二次根式$\sqrt{{a}^{2}}$=|a|后,研究了如下四个问题,其中错误的是( )
| A. | 在a>1的条件下化简代数式a+$\sqrt{{a}^{2}-2a+1}$的结果为2a-1 | |
| B. | a+$\sqrt{{a}^{2}-2a+1}$的值随a变化而变化,当a取某个数值时,上述代数式的值可以为$\frac{1}{2}$ | |
| C. | 当a+$\sqrt{{a}^{2}-2a+1}$的值恒为定值时,字母a的取值范围是a≤1 | |
| D. | 若$\sqrt{{a}^{2}-2a+1}$=($\sqrt{a-1}$)2,则字母a必须满足a≥1 |
 如图,把一张矩形纸片ABCD沿EF折叠后,点A落在CD边上的点A′处,点B落在点B′处.若∠1=115°,则∠2的度数为40°.
如图,把一张矩形纸片ABCD沿EF折叠后,点A落在CD边上的点A′处,点B落在点B′处.若∠1=115°,则∠2的度数为40°. 如图直线a∥b,PM⊥c,若∠1=50°,则∠2=40°.
如图直线a∥b,PM⊥c,若∠1=50°,则∠2=40°. 如图,有分别过A、B两个加油站的公路l1、l2相交于点O,现准备在∠A0B内部建一个油库,要求油库的位置点P满足到A、B两个加油站的距离相等,而且点P到两条公路l1、l2的距离也相等.请用尺规作图作出点P.(不写作法,保留作图痕迹)
如图,有分别过A、B两个加油站的公路l1、l2相交于点O,现准备在∠A0B内部建一个油库,要求油库的位置点P满足到A、B两个加油站的距离相等,而且点P到两条公路l1、l2的距离也相等.请用尺规作图作出点P.(不写作法,保留作图痕迹)