题目内容
20．
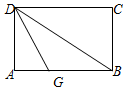如图，将矩形纸片ABCD折叠，先折出折痕（对角线）BD，再折叠，使边DA与对角线BD重合，得折痕DG，若AB=8，BC=6，则AG的长是3．
分析 根据勾股定理求出BD，根据角平分线的性质列出比例式，计算即可．
解答 解：由勾股定理得，DB=$\sqrt{A{D}^{2}+A{B}^{2}}$=10，
由折叠的性质可知，∠ADG=∠BDG，
∴$\frac{AG}{BG}$=$\frac{AD}{BD}$，即$\frac{AG}{8-AG}$=$\frac{6}{10}$，
解得，AG=3，
故答案为：3．
点评 本题考查的是翻转变换的性质、角平分线的性质，掌握翻转变换是一种对称变换，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等是解题的关键．
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
10．菱形两对角线长分别为24cm和10cm，则菱形的高为（ ） cm．
| A． | 13 | B． | $\frac{240}{13}$ | C． | 120 | D． | $\frac{120}{13}$ |
15．
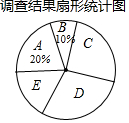2017年全国两会民生话题成为社会焦点．徐州市记者为了了解百姓“两会民生话题”的聚焦点，随机调查了徐州市部分市民，并对调查结果进行整理．绘制了如图所示的不完整的统计图表．
请根据图表中提供的信息解答下列问题：
（1）填空：m=40，n=100．扇形统计图中E组所占的百分比为15%；
（2）徐州市市区人口现有170万人，请你估计其中关注D组话题的市民人数；
（3）若在这次接受调查的市民中，随机抽查一人，则此人关注C组话题的概率是多少？
2017年全国两会民生话题成为社会焦点．徐州市记者为了了解百姓“两会民生话题”的聚焦点，随机调查了徐州市部分市民，并对调查结果进行整理．绘制了如图所示的不完整的统计图表．| 组别 | 焦点话题 | 频数（人数） |
| A | 食品安全 | 80 |
| B | 教育医疗 | m |
| C | 就业养老 | n |
| D | 生态环保 | 120 |
| E | 其他 | 60 |
（1）填空：m=40，n=100．扇形统计图中E组所占的百分比为15%；
（2）徐州市市区人口现有170万人，请你估计其中关注D组话题的市民人数；
（3）若在这次接受调查的市民中，随机抽查一人，则此人关注C组话题的概率是多少？
如图，已知线段AB=2，MN⊥AB于点M，且AM=BM，P是射线MN上一动点，E，D分别是PA，PB的中点，过点A，M，D的圆与BP的另一交点C（点C在线段BD上），连结AC，DE．
10．某数学兴趣小组在学习二次根式$\sqrt{{a}^{2}}$=|a|后，研究了如下四个问题，其中错误的是（ ）
| A． | 在a＞1的条件下化简代数式a+$\sqrt{{a}^{2}-2a+1}$的结果为2a-1 | |
| B． | a+$\sqrt{{a}^{2}-2a+1}$的值随a变化而变化，当a取某个数值时，上述代数式的值可以为$\frac{1}{2}$ | |
| C． | 当a+$\sqrt{{a}^{2}-2a+1}$的值恒为定值时，字母a的取值范围是a≤1 | |
| D． | 若$\sqrt{{a}^{2}-2a+1}$=（$\sqrt{a-1}$）2，则字母a必须满足a≥1 |