题目内容
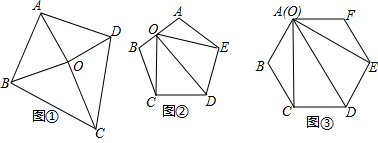
12. 如图所示.已知菱形ABCD的对角线AC,BD的交点为点O,AE⊥BC于点E.若菱形的周长为20cm,AC=6cm.求AE的长.
如图所示.已知菱形ABCD的对角线AC,BD的交点为点O,AE⊥BC于点E.若菱形的周长为20cm,AC=6cm.求AE的长.
分析 根据菱形的对角线互相垂直平分求出CO,再利用勾股定理列式求出BO,然后利用菱形的面积等于底乘以高和对角线乘积的一半列出方程求解即可.
解答 解:∵四边形ABCD是菱形,
∴CO=$\frac{1}{2}$AC=3cm,
∵菱形的周长为20cm,
∴BC=5cm,
∴BO=$\sqrt{B{C}^{2}-O{C}^{2}}$=4cm,
∴BD=8cm,
∴S菱形ABCD=$\frac{1}{2}$×BD•AC=BC•AE,
即$\frac{1}{2}$×6×8=5•AE,
解得AE=$\frac{24}{5}$cm.
答:AE的长是$\frac{24}{5}$cm.
点评 本题考查了菱形的性质,勾股定理,熟记菱形的对角线互相垂直平分是解题的关键,难点在于利用菱形的面积列出方程.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
20.下列叙述正确的是( )
| A. | 所有的直角三角形都相似 | B. | 所有的等腰三角形都相似 | ||
| C. | 所有的等腰直角三角形都相似 | D. | 所有的矩形都相似 |
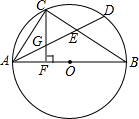 如图,AB是⊙O的直径,D是$\widehat{AB}$上一点,C是弧$\widehat{AD}$的中点,AD、BC相交于E,CF⊥AB,F为垂足,CF交AD于G,求证:CG=EG.
如图,AB是⊙O的直径,D是$\widehat{AB}$上一点,C是弧$\widehat{AD}$的中点,AD、BC相交于E,CF⊥AB,F为垂足,CF交AD于G,求证:CG=EG.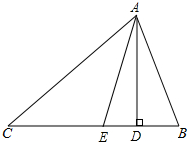 如图,在△ABC中,∠B>∠C,AD是高,AE是角平分线.猜想∠DAE与∠B和∠C的关系,并说明理由.
如图,在△ABC中,∠B>∠C,AD是高,AE是角平分线.猜想∠DAE与∠B和∠C的关系,并说明理由.