题目内容
7.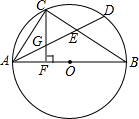 如图,AB是⊙O的直径,D是$\widehat{AB}$上一点,C是弧$\widehat{AD}$的中点,AD、BC相交于E,CF⊥AB,F为垂足,CF交AD于G,求证:CG=EG.
如图,AB是⊙O的直径,D是$\widehat{AB}$上一点,C是弧$\widehat{AD}$的中点,AD、BC相交于E,CF⊥AB,F为垂足,CF交AD于G,求证:CG=EG.
分析 连接CD,根据同弧所对的圆周角相等得到∠ABC=∠ADC=∠ACD,根据∠ACF+∠GCE=90°,∠CAD+∠GEC=90°,得到答案.
解答  证明:连接CD,
证明:连接CD,
∵C是$\widehat{AD}$的中点,
∴∠ABC=∠ADC=∠CAD,
∵AB为直径,∴∠ACB=90°,CF⊥AB,
∴∠ACF=∠ABC,
∴∠ACF=∠CAD,
∵∠ACF+∠GCE=90°,∠CAD+∠GEC=90°,
∴∠GCE=∠GEC,
∴CG=EG.
点评 本题考查的是圆周角定理的应用,掌握同弧所对的圆周角相等、直径所对的圆周角等于90°是解题的关键.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
18.在平面内有A、B两点,若以B点为原点建立平面直角坐标系,则点A的坐标为(2,5),若以A点为原点建立平面直角坐标系,则点B的坐标为( )
| A. | (-2,-5) | B. | (-2,5) | C. | (2,-5) | D. | (2,5) |
19.下列银行标志中是轴对称图形的个数有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
16.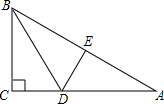 如图,在△ABC中,∠C=90°,BD平分∠ABC交AC于D,DE是AB的垂直平分线,DE=$\frac{1}{2}$BD,DE=1.5cm,则AC等于( )
如图,在△ABC中,∠C=90°,BD平分∠ABC交AC于D,DE是AB的垂直平分线,DE=$\frac{1}{2}$BD,DE=1.5cm,则AC等于( )
 如图,在△ABC中,∠C=90°,BD平分∠ABC交AC于D,DE是AB的垂直平分线,DE=$\frac{1}{2}$BD,DE=1.5cm,则AC等于( )
如图,在△ABC中,∠C=90°,BD平分∠ABC交AC于D,DE是AB的垂直平分线,DE=$\frac{1}{2}$BD,DE=1.5cm,则AC等于( )| A. | 3cm | B. | 7.5cm | C. | 6cm | D. | 4.5cm |
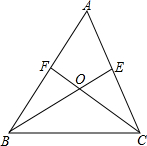 如图,在△ABC中,BE平分∠ABC,F是AB边上一点,CF交BE于点O,∠BOC=90°+$\frac{1}{2}$∠A,请你用推理的方法说明CF平分∠ACB.
如图,在△ABC中,BE平分∠ABC,F是AB边上一点,CF交BE于点O,∠BOC=90°+$\frac{1}{2}$∠A,请你用推理的方法说明CF平分∠ACB.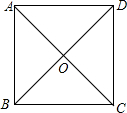 如图是一个边长为a的正方形.两条对角线AC与BD相交于O.观察此图并回答下面问题:
如图是一个边长为a的正方形.两条对角线AC与BD相交于O.观察此图并回答下面问题: 如图所示.已知菱形ABCD的对角线AC,BD的交点为点O,AE⊥BC于点E.若菱形的周长为20cm,AC=6cm.求AE的长.
如图所示.已知菱形ABCD的对角线AC,BD的交点为点O,AE⊥BC于点E.若菱形的周长为20cm,AC=6cm.求AE的长. 如图所示,若∠A+∠B+∠C+∠D+∠E+∠F=660°,求∠G+∠H的度数.
如图所示,若∠A+∠B+∠C+∠D+∠E+∠F=660°,求∠G+∠H的度数.