题目内容
17.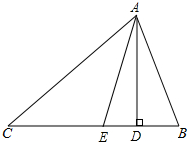 如图,在△ABC中,∠B>∠C,AD是高,AE是角平分线.猜想∠DAE与∠B和∠C的关系,并说明理由.
如图,在△ABC中,∠B>∠C,AD是高,AE是角平分线.猜想∠DAE与∠B和∠C的关系,并说明理由.
分析 先根据三角形内角和得到∠CAB=180°-∠B-∠C,再根据角平分线与高线的定义得到∠CAE=$\frac{1}{2}$∠CAB=90°-$\frac{1}{2}∠B-\frac{1}{2}∠C$,∠ADC=90°,则∠CAD=90°-∠C,然后利用∠DAE=∠CAD-∠CAE计算即可.
解答 解:$∠DAE=\frac{1}{2}(∠B-∠C)$,理由如下:
在△ABC中,∠CAB=180°-∠B-∠C,
∵AE是角平分线,
∴∠CAE=$\frac{1}{2}$∠CAB=90°-$\frac{1}{2}∠B-\frac{1}{2}∠C$,
∵AD是高,
∴∠CAD=90°-∠C,
∴∠DAE=∠CAD-∠CAE=90°-∠C-(90°-$\frac{1}{2}∠B-\frac{1}{2}∠C$)=$\frac{1}{2}(∠B-∠C)$
点评 本题考查了三角形内角和定理:三角形内角和为180°.也考查了三角形外角性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.在下列说法中,正确的是( )
| A. | 如果两个三角形全等,则它们必是关于直线成轴对称的图形 | |
| B. | 如果两个三角形关于某直线成轴对称,那么它们是全等三角形 | |
| C. | 等腰三角形底边中线是对称轴 | |
| D. | 一条线段是关于经过该线段中点的直线成轴对称的图形 |
 如图,点A、B、C在⊙O上,点D在圆外,CD、BD分别交⊙O于点E、F,比较∠BAC与∠BDC的大小,并说明理由.
如图,点A、B、C在⊙O上,点D在圆外,CD、BD分别交⊙O于点E、F,比较∠BAC与∠BDC的大小,并说明理由.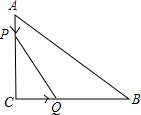 如图,△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从A沿AC边向C点以1cm/s的速度移动,在C点停止,点Q从C点开始沿CB边向点B以2cm/s的速度移动,在B点停止.
如图,△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从A沿AC边向C点以1cm/s的速度移动,在C点停止,点Q从C点开始沿CB边向点B以2cm/s的速度移动,在B点停止. 如图,已知在△ABC中,中线BD、CE交于点O,且△ABC的面积为60,试求四边形ADOE的面积.
如图,已知在△ABC中,中线BD、CE交于点O,且△ABC的面积为60,试求四边形ADOE的面积. 如图所示.已知菱形ABCD的对角线AC,BD的交点为点O,AE⊥BC于点E.若菱形的周长为20cm,AC=6cm.求AE的长.
如图所示.已知菱形ABCD的对角线AC,BD的交点为点O,AE⊥BC于点E.若菱形的周长为20cm,AC=6cm.求AE的长. 如图,已知在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线DE交AC于点E,交BC于点D,求证:BD=2DC.
如图,已知在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线DE交AC于点E,交BC于点D,求证:BD=2DC.