题目内容
2.在△ABC中.(1)∠C=80°,∠A=30°,则∠B=70°;
(2)∠A=70°,∠B=∠C,则∠B=55°;
(3)在△ABC中,∠A:∠B:∠C=1:2:3,△ABC是直角三角形.
分析 (1)根据三角形内角和是180度即可求得∠B的度数;
(2)根据三角形的内角和等于180°,通过列方程即可求出∠B的度数;
(3)根据比例设∠A、∠B、∠C分别为k、2k、3k,然后根据三角形的内角和等于180°列式求出∠C,作出判断即可.
解答 (1)在△ABC中,∠C=80°,∠A=30°,
则由三角形内角和定理知,
∠B=180°-∠A-∠C=180°-30°-80°=70°.
故答案是:70°;
(2)设∠B=x°,则∠C=x°,
∵∠A+∠B+∠C=180°,
∴x+x+70=180,
∴x=55,
∴∠B=55°.
故答案为:55°;
(3)设∠A、∠B、∠C分别为k、2k、3k,
则k+2k+3k=180°,
解得k=30°,
所以,∠C=3×30°=90°,
这个三角形是直角三角形.
故答案为:直角.
点评 本题考查了三角形内角和定理,解答(3)时利用“设k法”用k表示出∠A、∠B、∠C可以使运算更加简便.

练习册系列答案
相关题目
 如图,在长方形ABCD内,直线EF与AB边平行,GH与BC边平行,AB与GH相交于O点,已知AG=5厘米,AE=2厘米,FC=6厘米,HC=10厘米,那么△BOD的面积是25平方厘米.
如图,在长方形ABCD内,直线EF与AB边平行,GH与BC边平行,AB与GH相交于O点,已知AG=5厘米,AE=2厘米,FC=6厘米,HC=10厘米,那么△BOD的面积是25平方厘米.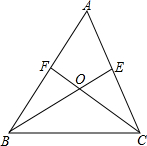 如图,在△ABC中,BE平分∠ABC,F是AB边上一点,CF交BE于点O,∠BOC=90°+$\frac{1}{2}$∠A,请你用推理的方法说明CF平分∠ACB.
如图,在△ABC中,BE平分∠ABC,F是AB边上一点,CF交BE于点O,∠BOC=90°+$\frac{1}{2}$∠A,请你用推理的方法说明CF平分∠ACB.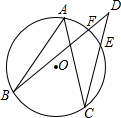 如图,点A、B、C在⊙O上,点D在圆外,CD、BD分别交⊙O于点E、F,比较∠BAC与∠BDC的大小,并说明理由.
如图,点A、B、C在⊙O上,点D在圆外,CD、BD分别交⊙O于点E、F,比较∠BAC与∠BDC的大小,并说明理由.



 如图所示.已知菱形ABCD的对角线AC,BD的交点为点O,AE⊥BC于点E.若菱形的周长为20cm,AC=6cm.求AE的长.
如图所示.已知菱形ABCD的对角线AC,BD的交点为点O,AE⊥BC于点E.若菱形的周长为20cm,AC=6cm.求AE的长.