题目内容
16.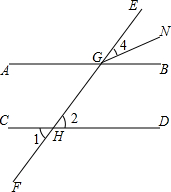 下面是某同学给出一种证法,请你将解答中缺少的条件、结论或证明理由补充完整:
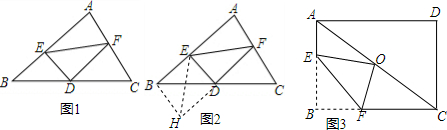
下面是某同学给出一种证法,请你将解答中缺少的条件、结论或证明理由补充完整:证明:∵CD与EF相交于点H(已知)
∴∠1=∠2(对顶角相等)
∵AB∥CD(已知)
∴∠2=∠EGB(两直线平行,同位角相等)
∵GN是∠EGB的平分线,(已知)
∴∠4=$\frac{1}{2}$∠BGE (角平分线定义)
∵∠1=∠2,∠2=∠EGB(已证)
∴∠1=∠EGB(等量代换)
∵$∠4=\frac{1}{2}$∠EGB(已证)
∴∠4=$\frac{1}{2}$∠1(等量代换)
分析 由CD与EF相交于点H得到∠1=∠2,根据平行线的性质∠2=∠EGB,由角平分线的性质得到∠4=$\frac{1}{2}∠$BGE然后根据等量代换得到结论.
解答 证明:∵CD与EF相交于点H(已知)
∴∠1=∠2(对顶角相等)
∵AB∥CD(已知)
∴∠2=∠EGB(两直线平行,同位角相等)
∵GN是∠EGB的平分线,(已知)
∴∠4=$\frac{1}{2}∠$BGE(角平分线定义)
∵∠1=∠2,∠2=∠EGB(已证)
∴∠1=∠EGB(等量代换)
∵$∠4=\frac{1}{2}∠$EGB,(已证)
∴∠4=$\frac{1}{2}$∠1(等量代换),
故答案为:对顶角相等,两直线平行,同位角相等,$\frac{1}{2}$∠EGB,等量代换,∠4=$\frac{1}{2}$∠EGB.
点评 本题考查了平行线的性质,角平分线的性质,对顶角的性质,熟练掌握性质定理是解题的关键.

练习册系列答案
相关题目
7.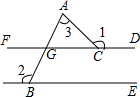 如图,已知FD∥BE,则∠1+∠2-∠3的值为( )
如图,已知FD∥BE,则∠1+∠2-∠3的值为( )
 如图,已知FD∥BE,则∠1+∠2-∠3的值为( )
如图,已知FD∥BE,则∠1+∠2-∠3的值为( )| A. | 90° | B. | 135° | C. | 150° | D. | 180° |