题目内容
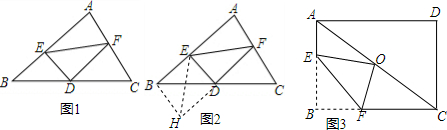
5.阅读下面材料:小明遇到这样一个问题:如图1,在△ABC中,D为BC中点,E、F分别为AB、AC上一点,且ED⊥DF,求证:BE+CF>EF.
小明发现,延长FD到点H,使DH=FD,连结BH、EH,构造△BDH和△EFH,通过证明△BDH与△CDF全等、△EFH为等腰三角形,利用△BEH使问题得以解决(如图2).
参考小明思考问题的方法,解决问题:
如图3,在矩形ABCD中,O为对角线AC中点,将矩形ABCD翻折,使点B恰好与点O重合,EF为折痕,猜想EF、AE、FC之间的数量关系?并证明你的猜想.
分析 猜想:EF2=AE2+CF2,延长EO交CD于点H,连结FH,首先证明△AEO≌△CHO,进而可得EO=HO,CH=AE,由折叠的性质可得△EFO≌△EFB,所以∠EOF=∠B=90°,继而在△FCH中,由勾股定理得FH2=CH2+FC2,即EF2=AE2+CF2问题得证.
解答 解: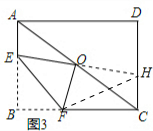 猜想:EF2=AE2+CF2,
猜想:EF2=AE2+CF2,
理由如下:延长EO交CD于点H,连结FH.
∵四边形ABCD是矩形
∴AB∥DC.∠B=90°
∴∠EAO=∠HCO.
∵O为对角线AC中点,
∴AO=CO.
∵∠BOE=∠COH,
∴△AEO≌△CHO.
∴EO=HO,CH=AE,
由题意可知△EFO≌△EFB.
∴∠EOF=∠B=90°.
∴OF垂直平分EH.
∴FH=EF
在△FCH中,由勾股定理得FH2=CH2+FC2,
∴EF2=AE2+CF2.
点评 本题考查了全等三角形的判定和性质、矩形的性质勾股定理的运用以及折叠的性质,解题的关键是正确条件辅助线构造全等三角形.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
13.某商场经销甲、乙两种商品,甲种商品每件进价15元,售价20元;乙种商品每件进价35元,售价45元.
(1)若该商场同时购进甲、乙两种商品共100件,恰好用去2700元,求购进甲、乙两种商品各多少件?
(2)该商场为使甲、乙两种商品共100件的总利润不少于750元,且不超过760元,请你通过计算求出该商场所有的进货方案;
(3)在“五•一”黄金周期间,该商场对甲、乙两种商品进行如下优惠促销活动:
按上述优惠条件,若贝贝第一天只购买甲种商品一次性付款200元,第二天只购买乙种商品打折后一次性付款324元,那么这两天他在该商场购买甲、乙两种商品各多少件?
(1)若该商场同时购进甲、乙两种商品共100件,恰好用去2700元,求购进甲、乙两种商品各多少件?
(2)该商场为使甲、乙两种商品共100件的总利润不少于750元,且不超过760元,请你通过计算求出该商场所有的进货方案;
(3)在“五•一”黄金周期间,该商场对甲、乙两种商品进行如下优惠促销活动:
| 打折前一次性购物总金额 | 优惠措施 |
| 不超过300元 | 不优惠 |
| 超过300元且不超过400元 | 售价打九折 |
| 超过400元 | 售价打八折 |
10. 某校随机抽取200名学生,对他们喜欢的图书类型进行问卷调查,统计结果如图.根据图中信息,估计该校2000名学生中喜欢文学类书籍的人数是( )
某校随机抽取200名学生,对他们喜欢的图书类型进行问卷调查,统计结果如图.根据图中信息,估计该校2000名学生中喜欢文学类书籍的人数是( )
 某校随机抽取200名学生,对他们喜欢的图书类型进行问卷调查,统计结果如图.根据图中信息,估计该校2000名学生中喜欢文学类书籍的人数是( )
某校随机抽取200名学生,对他们喜欢的图书类型进行问卷调查,统计结果如图.根据图中信息,估计该校2000名学生中喜欢文学类书籍的人数是( )| A. | 800 | B. | 600 | C. | 400 | D. | 200 |

 下面是某同学给出一种证法,请你将解答中缺少的条件、结论或证明理由补充完整:
下面是某同学给出一种证法,请你将解答中缺少的条件、结论或证明理由补充完整: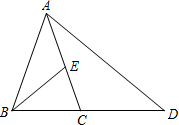 已知:如图,在△ABC中,AB=AC=6,BC=4,D是边BC延长线上一点,E是边AC上一点,且∠EBC=∠D,设CE=x,CD=y.
已知:如图,在△ABC中,AB=AC=6,BC=4,D是边BC延长线上一点,E是边AC上一点,且∠EBC=∠D,设CE=x,CD=y.