题目内容
7.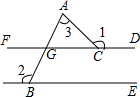 如图,已知FD∥BE,则∠1+∠2-∠3的值为( )
如图,已知FD∥BE,则∠1+∠2-∠3的值为( )| A. | 90° | B. | 135° | C. | 150° | D. | 180° |
分析 先根据平行线的性质得出∠2+∠FGB=180°,再由对顶角相等得出∠AGC=∠FGB,故∠2+∠AGC=180°,∠AGC=180°-∠2,根据∠1=∠3+∠AGC,可知∠1-∠3=∠AGC,进而可得出结论.
解答 解:∵DF∥BE,
∴∠2+∠FGB=180°,
∵∠AGC=∠FGB,
∴∠2+∠AGC=180°,
∴∠AGC=180°-∠2,
∵∠1=∠3+∠AGC,
∴∠1-∠3=∠AGC,
∴∠1+∠2-∠3=∠AGC+180°-∠AGC=180°.
故选D.
点评 本题考查了三角形外角性质和平行线性质的应用,注意:两直线平行,同旁内角互补.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
18.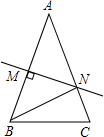 如图,在三角形ABC中,AB=AC,∠A=36°,AB的垂直平分线MN交AB于点M,交AC于点N,下面结论:①BN平分∠ABC;②△BCN是等腰三角形;③△BMN≌△BCN;④△BCN的周长等于AB+BC,其中正确的结论是( )
如图,在三角形ABC中,AB=AC,∠A=36°,AB的垂直平分线MN交AB于点M,交AC于点N,下面结论:①BN平分∠ABC;②△BCN是等腰三角形;③△BMN≌△BCN;④△BCN的周长等于AB+BC,其中正确的结论是( )
 如图,在三角形ABC中,AB=AC,∠A=36°,AB的垂直平分线MN交AB于点M,交AC于点N,下面结论:①BN平分∠ABC;②△BCN是等腰三角形;③△BMN≌△BCN;④△BCN的周长等于AB+BC,其中正确的结论是( )
如图,在三角形ABC中,AB=AC,∠A=36°,AB的垂直平分线MN交AB于点M,交AC于点N,下面结论:①BN平分∠ABC;②△BCN是等腰三角形;③△BMN≌△BCN;④△BCN的周长等于AB+BC,其中正确的结论是( )| A. | ①②③ | B. | ①②④ | C. | ②③④ | D. | ①③④ |
2.下列各数中,是无理数的是( )
| A. | $\frac{22}{7}$ | B. | 0.101001 | C. | $\sqrt{81}$ | D. | $\sqrt{32}$ |
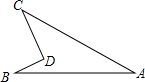 如图,∠BDC=98°,∠ACD=38°,∠ABD=23°,则∠A的度数是37°.
如图,∠BDC=98°,∠ACD=38°,∠ABD=23°,则∠A的度数是37°.
 已知:线段a,b.求作:△ABC,使AB=AC=b,且BC边上的高AD=a(不写作法,只保留作图痕迹)
已知:线段a,b.求作:△ABC,使AB=AC=b,且BC边上的高AD=a(不写作法,只保留作图痕迹)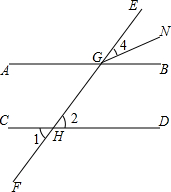 下面是某同学给出一种证法,请你将解答中缺少的条件、结论或证明理由补充完整:
下面是某同学给出一种证法,请你将解答中缺少的条件、结论或证明理由补充完整: