题目内容
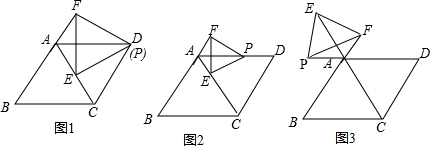
8.【提出问题】(1)已知:菱形ABCD的变长为4,∠ADC=60°,△PEF为等边三角形,当点P与点D重合,点E在对角线AC上时(如图1所示),求AE+AF的值;
【类比探究】
(2)在上面的问题中,如果把点P沿DA方向移动,使PD=1,其余条件不变(如图2),你能发现AE+AF的值是多少?请直接写出你的结论;
【拓展迁移】
(3)在原问题中,当点P在线段DA的延长线上,点E在CA的延长线上时(如图3),设AP=m,则线段AE、AF的长与m有怎样的数量关系?请说明理由.
分析 (1)首先判断出△ACD是等边三角形,即可判断出AC=AD=4;然后根据全等三角形判定的方法,判断出△APF≌△CPE,即可判断出CE=AF,据此求出AE+AF的值是多少即可.
(2)首先取AC上的点G,使得CG=PD=1,判断出GP∥CD,即可判断出∠APF=∠GPE;然后根据全等三角形判定的方法,判断出△APF≌△GPE,即可判断出GE=AF,据此求出AE+AF的值是多少即可.
(3)首先作PH∥CD交CE于点H,判断出△AHP∽△ACD,即可判断出△AHP是等边三角形;然后根据全等三角形判定的方法,判断出△APF≌△HPE,即可判断出AF=HE,再根据PA=AH,可得AE=PA+AF,所以AE-AF=m,据此解答即可.
解答 解:(1)如图1, ,
,
∵四边形ABCD是菱形,
∴PA=PC,
∵∠ADC=60°,
∴△ACD是等边三角形,
∴AC=AD=4,
又∵△PEF为等边三角形,
∴∠ADC=∠EPF=60°,
∴∠APF=∠CPE,
在△APF和△CPE中,
$\left\{\begin{array}{l}{AP=CP}\\{∠APF=∠CPE}\\{PF=PE}\end{array}\right.$
∴△APF≌△CPE,
∴CE=AF,
∴AE+AF=AE+CE=AC=4,
即AE+AF的值是4.
(2)如图2,点G是AC上的一点,且满足CG=PD=1, ,
,
∵CG=PD,AC=AD,
∴AG=AP,
∴$\frac{AG}{CG}=\frac{AP}{PD}$,
∴GP∥CD,
∴∠GPA=∠CDA=60°,
又∵EPF=60°,
∴∠APF=∠GPE,
在△APF和△GPE中,
$\left\{\begin{array}{l}{AP=GP}\\{∠APF=∠GPE}\\{FP=EP}\end{array}\right.$
∴△APF≌△GPE,
∴GE=AF,
∴AE+AF=AE+GE=AG=AC-CG=4-1=3,
即AE+AF的值是3.
(3)如图3,作PH∥CD交CE于点H, ,
,
由(1),可得△ACD是等边三角形,
∵PH∥CD,
∴△AHP∽△ACD,
∴△AHP是等边三角形,
∴PA=PH,∠APH=∠EPF=60°,
∴∠FPA=∠EPH,
在△APF和△HPE中,
$\left\{\begin{array}{l}{PA=PH}\\{∠FPA=∠EPH}\\{PF=PE}\end{array}\right.$
∴△APF≌△HPE,
∴AF=HE,
又∵PA=AH,
∴AE=PA+AF,
∴AE-AF=m.
点评 (1)此题主要考查了四边形综合题,考查了分析推理能力,考查了分类讨论思想的应用,考查了数形结合思想的应用,要熟练掌握.
(2)此题还考查了全等三角形的判定和性质的应用,要熟练掌握,解答此题的关键是要明确:①判定定理1:SSS--三条边分别对应相等的两个三角形全等.②判定定理2:SAS--两边及其夹角分别对应相等的两个三角形全等.③判定定理3:ASA--两角及其夹边分别对应相等的两个三角形全等.④判定定理4:AAS--两角及其中一个角的对边对应相等的两个三角形全等.⑤判定定理5:HL--斜边与直角边对应相等的两个直角三角形全等.
(3)此题还考查了三角形相似的判定和性质的应用,以及菱形的性质和应用,要熟练掌握.

 阅读快车系列答案
阅读快车系列答案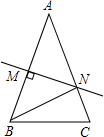 如图,在三角形ABC中,AB=AC,∠A=36°,AB的垂直平分线MN交AB于点M,交AC于点N,下面结论:①BN平分∠ABC;②△BCN是等腰三角形;③△BMN≌△BCN;④△BCN的周长等于AB+BC,其中正确的结论是( )
如图,在三角形ABC中,AB=AC,∠A=36°,AB的垂直平分线MN交AB于点M,交AC于点N,下面结论:①BN平分∠ABC;②△BCN是等腰三角形;③△BMN≌△BCN;④△BCN的周长等于AB+BC,其中正确的结论是( )| A. | ①②③ | B. | ①②④ | C. | ②③④ | D. | ①③④ |
(1)若该商场同时购进甲、乙两种商品共100件,恰好用去2700元,求购进甲、乙两种商品各多少件?
(2)该商场为使甲、乙两种商品共100件的总利润不少于750元,且不超过760元,请你通过计算求出该商场所有的进货方案;
(3)在“五•一”黄金周期间,该商场对甲、乙两种商品进行如下优惠促销活动:
| 打折前一次性购物总金额 | 优惠措施 |
| 不超过300元 | 不优惠 |
| 超过300元且不超过400元 | 售价打九折 |
| 超过400元 | 售价打八折 |
 已知:线段a,b.求作:△ABC,使AB=AC=b,且BC边上的高AD=a(不写作法,只保留作图痕迹)
已知:线段a,b.求作:△ABC,使AB=AC=b,且BC边上的高AD=a(不写作法,只保留作图痕迹)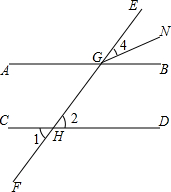 下面是某同学给出一种证法,请你将解答中缺少的条件、结论或证明理由补充完整:
下面是某同学给出一种证法,请你将解答中缺少的条件、结论或证明理由补充完整: