题目内容
10.关于x的一元二次方程a(b-c)x2+b(c-a)x+c(a-b)=0必有一个根为( )| A. | x=0 | B. | x=1 | C. | x=-1 | D. | x=2 |
分析 根据方程的解的定义,将选项中x的值一一代入进行验证即可.
解答 解:A、把x=0代入得到:c(a-b)=0,若c≠0,a≠b时,该等式不成立,即x=0不一定是原方程的解,故本选项错误;
B、把x=1代入得到:左边=a(b-c)+b(c-a)+c(a-b)=0=右边,即x=1一定是原方程的解,故本选项正确;
C、把x=-1代入得到:a(b-c)-b(c-a)+c(a-b)=2b(a-c)=0,若b≠0,a≠c时,该等式不成立,即x=-1不一定是原方程的解,故本选项错误;
D、把x=2代入得到:4a(b-c)+2b(c-a)+c(a-b)=2ab-3ac+bc=0,若a=b=c=0时,该等式成立,即x=2不一定是原方程的解,故本选项错误;
故选:B.
点评 本题考查了一元二次方程的解的定义.能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.又因为只含有一个未知数的方程的解也叫做这个方程的根,所以,一元二次方程的解也称为一元二次方程的根.

练习册系列答案
相关题目
 a、b、c三个数在数轴上的对应位置如图所示,化简:|a|-|a+b|+|c-b|+|a+c|.
a、b、c三个数在数轴上的对应位置如图所示,化简:|a|-|a+b|+|c-b|+|a+c|.
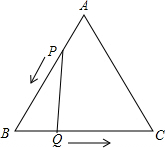 如图所示,△ABC是边长3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动.设点P的运动时间为t(s),解答下列问题:
如图所示,△ABC是边长3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动.设点P的运动时间为t(s),解答下列问题: 将正奇数按如右上图所示规律排列下去.若用有序数对(n,m)表示实数9,则(6,3)表示的数是35.2011是(45,16).
将正奇数按如右上图所示规律排列下去.若用有序数对(n,m)表示实数9,则(6,3)表示的数是35.2011是(45,16).