题目内容
4.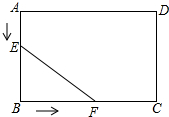 如图,在矩形ABCD中,AB=5cm,BC=7cm,点E从点A出发,沿AB方向以1cm/s的速度向点B移动,同时,点F从点B出发,沿BC方向以2cm/s的速度向点C移动,当点F到达点C时,两点同时停止运动,设运动时间为t秒.
如图,在矩形ABCD中,AB=5cm,BC=7cm,点E从点A出发,沿AB方向以1cm/s的速度向点B移动,同时,点F从点B出发,沿BC方向以2cm/s的速度向点C移动,当点F到达点C时,两点同时停止运动,设运动时间为t秒.(1)当t为何值时,△BEF的面积为5cm2?
(2)当t为何值时,△BEF与△ABD相似?
分析 (1)用t表示出BE及BF的长,再由三角形的面积公式即可得出结论;
(2)分△BEF∽△ABD与△BEF与△ADB两种情况进行讨论即可.
解答 解:(1)∵AB=5cm,BC=7cm,点E从点A出发,沿AB方向以1cm/s的速度向点B移动,同时,点F从点B出发,沿BC方向以2cm/s的速度向点C移动,
∴BE=5-t,BF=2t.
∵△BEF的面积为5cm2,
∴$\frac{1}{2}$BF•BE=5,即$\frac{1}{2}$×2t×(5-t)=5,解得t1=$\frac{5+\sqrt{5}}{2}$(舍去),t2=$\frac{5-\sqrt{5}}{2}$.
答:当t=$\frac{5-\sqrt{5}}{2}$时,△BEF的面积为5cm2;
(2)∵BE=5-t,BF=2t,
∴当△BEF∽△ABD时,$\frac{BE}{AB}$=$\frac{BF}{AD}$,即$\frac{5-t}{5}$=$\frac{2t}{7}$,解得t=$\frac{35}{17}$;
当△BEF与△ADB时,$\frac{BE}{AD}$=$\frac{BF}{AB}$,即$\frac{5-t}{7}$=$\frac{2t}{5}$,解得t=$\frac{25}{19}$.
综上所述,当t为$\frac{35}{17}$秒或$\frac{25}{19}$秒时,BEF与△ABD相似.
点评 本题考查的是相似三角形的判定,在解答此题时要注意进行分类讨论,不要漏解.

练习册系列答案
相关题目
12.某自行车厂计划平均每天生产200辆,但是由于种种原因,实际每天生产量与计划量相比有出入.表是某周的生产情况(超产记为正,减产记为负):
(1)根据记录的数据可知该厂星期三生产自行车多少辆?
(2)产量最多的一天比产量最少的一天多生产自行车多少辆?
(3)根据记录的数据可知该厂本周实际共生产自行车多少辆?
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | +6 | -3 | -8 | +14 | -10 | +15 | -4 |
(2)产量最多的一天比产量最少的一天多生产自行车多少辆?
(3)根据记录的数据可知该厂本周实际共生产自行车多少辆?
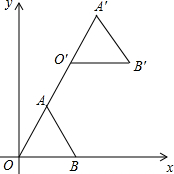 已知:如图,在平面直角坐标系中,正三角形OAB的顶点B的坐标为(2,0),点A在第一象限内
已知:如图,在平面直角坐标系中,正三角形OAB的顶点B的坐标为(2,0),点A在第一象限内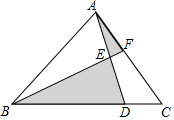 三角形ABC的面积为10cm2,AE=$\frac{1}{2}$AD,BD=3DC,求阴影部分的面积.
三角形ABC的面积为10cm2,AE=$\frac{1}{2}$AD,BD=3DC,求阴影部分的面积.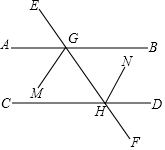 如图,AB∥CD,MG平分∠AGF,NH平分∠EHD,那么GM∥HN,请说明理由.
如图,AB∥CD,MG平分∠AGF,NH平分∠EHD,那么GM∥HN,请说明理由. 如图,已知△ABC中,AB=AC,把△ABC绕A点顺时针方向旋转得到△ADE,连接BD,CE交于点F,求证:△AEC≌△ADB.
如图,已知△ABC中,AB=AC,把△ABC绕A点顺时针方向旋转得到△ADE,连接BD,CE交于点F,求证:△AEC≌△ADB.