题目内容
17.若a:b:c=3:2:5,则$\frac{a+2b-c}{a-b+c}$=$\frac{1}{3}$;若3x=2y,则$\frac{2x-y}{x+3y}$=$\frac{1}{11}$;若$\frac{x}{x+y}$=$\frac{3}{5}$,则$\frac{x}{y}$=$\frac{3}{2}$.分析 根据a:b:c=3:2:5,用含k的式子表示a,b,c各值,即可解答;由3x=2y,用含k的式子表示x,y的值,即可求出分式的值,根据$\frac{x}{x+y}=\frac{3}{5}$,可得2x=3y,即可解答.
解答 解:∵a:b:c=3:2:5,
∴设a=3k,b=2k,c=5k,
∴原式=$\frac{3k+4k-5k}{3k-2k+5k}$=$\frac{2k}{6k}$=$\frac{1}{3}$;
由3x=2y可知,x:y=2:3,
故设x=2k,y=3k,
∴原式=$\frac{4k-3k}{2k+9k}$=$\frac{k}{11k}$=$\frac{1}{11}$;
∵$\frac{x}{x+y}=\frac{3}{5}$,
∴2x=3y,
∴$\frac{x}{y}=\frac{3}{2}$,
故答案为:$\frac{1}{3}$,$\frac{1}{11}$,$\frac{3}{2}$.
点评 本题主要考查比例的基本性质,解决此类题目时,用含k的式子表示出各字母的值,再代入求值即可.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
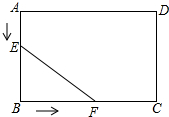 如图,在矩形ABCD中,AB=5cm,BC=7cm,点E从点A出发,沿AB方向以1cm/s的速度向点B移动,同时,点F从点B出发,沿BC方向以2cm/s的速度向点C移动,当点F到达点C时,两点同时停止运动,设运动时间为t秒.
如图,在矩形ABCD中,AB=5cm,BC=7cm,点E从点A出发,沿AB方向以1cm/s的速度向点B移动,同时,点F从点B出发,沿BC方向以2cm/s的速度向点C移动,当点F到达点C时,两点同时停止运动,设运动时间为t秒.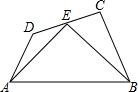 如图,在四边形ABCD中,∠BCD=90°,E为CD的中点,连接AE、BE,AE=BE,AE⊥BE,若BC-CD=2,AD=$\sqrt{74}$,则AB边的长为13$\sqrt{2}$.
如图,在四边形ABCD中,∠BCD=90°,E为CD的中点,连接AE、BE,AE=BE,AE⊥BE,若BC-CD=2,AD=$\sqrt{74}$,则AB边的长为13$\sqrt{2}$. “三月三,放风筝”如图是小东同学自己做的风筝,他根据AB=AD,BC=DC,不用度量,就知道∠ABC=∠ADC.请用所学的知识给予说明.
“三月三,放风筝”如图是小东同学自己做的风筝,他根据AB=AD,BC=DC,不用度量,就知道∠ABC=∠ADC.请用所学的知识给予说明.