题目内容
10.解方程组:$\left\{\begin{array}{l}{x^2}-2xy-3{y^2}=0\\{x^2}-xy+{y^2}=3.\end{array}\right.$.分析 先把第一个方程利用因式分解的方法化为x-3y=0或x+y=0,则原方程可转化为$\left\{\begin{array}{l}{x-3y=0}\\{{x}^{2}-xy+{y}^{2}=3}\end{array}\right.$或$\left\{\begin{array}{l}{x+y=0}\\{{x}^{2}-xy+{y}^{2}=3}\end{array}\right.$,然后利用代入法解两个二元二次方程组即可.
解答 解:$\left\{\begin{array}{l}{{x}^{2}-2xy-3{y}^{2}=0①}\\{{x}^{2}-xy+{y}^{2}=3②}\end{array}\right.$,
由①得(x-3y)(x+y)=0,
所以x-3y=0或x+y=0,
所以原方程可转化为$\left\{\begin{array}{l}{x-3y=0}\\{{x}^{2}-xy+{y}^{2}=3}\end{array}\right.$或$\left\{\begin{array}{l}{x+y=0}\\{{x}^{2}-xy+{y}^{2}=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=\frac{3\sqrt{21}}{7}}\\{y=\frac{\sqrt{21}}{7}}\end{array}\right.$或$\left\{\begin{array}{l}{x=-\frac{3\sqrt{21}}{7}}\\{y=-\frac{\sqrt{21}}{7}}\end{array}\right.$或$\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$或$\left\{\begin{array}{l}{x=-1}\\{y=1}\end{array}\right.$,
所以原方程组的解为$\left\{\begin{array}{l}{x=\frac{3\sqrt{21}}{7}}\\{y=\frac{\sqrt{21}}{7}}\end{array}\right.$或$\left\{\begin{array}{l}{x=-\frac{3\sqrt{21}}{7}}\\{y=-\frac{\sqrt{21}}{7}}\end{array}\right.$或$\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$或$\left\{\begin{array}{l}{x=-1}\\{y=1}\end{array}\right.$.
点评 本题考查了高次方程:通过适当的方法,把高次方程化为次数较低的方程求解.所以解高次方程一般要降次,即把它转化成二次方程或一次方程.也有的通过因式分解来解.

 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案| A. | b2-4ac<0 | B. | b2-4ac>0 | C. | b2-4ac≥0 | D. | b2-4ac≤0 |
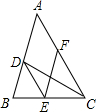 如图,CD是△ABC的角平分线,点E、F分别在BC、AC上,且DE∥AC,FE∥AB.
如图,CD是△ABC的角平分线,点E、F分别在BC、AC上,且DE∥AC,FE∥AB.