题目内容
4．若方程组$\left\{\begin{array}{l}{ax+y=0}\\{2x+by=6}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$，则a+b=（ ）| A． | 2 | B． | -2 | C． | 0 | D． | 4 |
分析 根据方程组$\left\{\begin{array}{l}{ax+y=0}\\{2x+by=6}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$，可以求得a、b的值，从而可以求得a+b的值．
解答 解：∵方程组$\left\{\begin{array}{l}{ax+y=0}\\{2x+by=6}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$，
∴$\left\{\begin{array}{l}{a-2=0}\\{2-2b=6}\end{array}\right.$，
解得，a=2，b=-2，
∴a+b=2+（-2）=0，
故选C．
点评 本题考查二元一次方程组的解，解题的关键是明确题意，找出所求问题需要的条件．
练习册系列答案
孟建平小学滚动测试系列答案
黄冈天天练口算题卡系列答案
相关题目
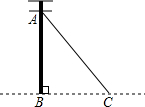如图，AC是电杆AB的一根拉线，测得BC=6，tan∠ACB=$\frac{4}{3}$，则拉线AC的长为10．
学校操场旁边一棵水杉树被大风吹断，如图测得树顶与水平地面刚好成60度夹角，且离树的底端5米，求这棵树原来有多高？（结果保留整数，$\sqrt{3}$≈1.732，$\sqrt{2}$≈1.414）
数a、b、c在数轴上对应的位置如图所示，化简|a+c|-|a|+|-b|．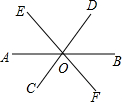
直线AB，CD，EF相交于点O，如图．