题目内容
12.探究问题:(1)方法感悟:
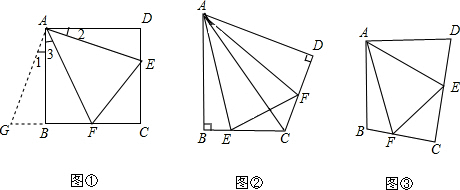
如图①,在正方形ABCD中,点E,F分别为DC,BC边上的点,且满足∠EAF=45°,连接EF,求证DE+BF=EF.
感悟解题方法,并完成下列填空:
将△ADE绕点A顺时针旋转90°得到△ABG,此时AB与AD重合,由旋转可得:
AB=AD,BG=DE,∠1=∠2,∠ABG=∠D=90°,
∴∠ABG+∠ABF=90°+90°=180°,
因此,点G,B,F在同一条直线上.
∵∠EAF=45°∴∠2+∠3=∠BAD-∠EAF=90°-45°=45°.
∵∠1=∠2,∴∠1+∠3=45°.
即∠GAF=∠FAE.
又AG=AE,AF=AF
∴△GAF≌△EAF.
∴GF=EF,故DE+BF=EF.
(2)方法迁移:
如图②,将Rt△ABC沿斜边翻折得到△ADC,点E,F分别为DC,BC边上的点,且∠EAF=$\frac{1}{2}$∠DAB.试猜想DE,BF,EF之间有何数量关系,并证明你的猜想.
(3)问题拓展:
如图③,在四边形ABCD中,AB=AD,E,F分别为DC,BC上的点,满足∠EAF=$\frac{1}{2}$∠DAB,试猜想当∠B与∠D满足什么关系时,可使得DE+BF=EF.请直接写出你的猜想(不必说明理由).
分析 (1)利用角之间的等量代换得出∠GAF=∠FAE,再利用SAS得出△GAF≌△EAF,得出答案;
(2)将△ADE顺时针旋转90°得到△ABG,再证明△AGF≌△AEF,即可得出答案;
(3)根据角之间关系,只要满足∠B+∠D=180°时,就可以得出三角形全等,即可得出答案.
解答 解:(1)如图①所示;
根据等量代换得出∠GAF=∠FAE,
利用SAS得出△GAF≌△EAF,
∴GF=EF,
故答案为:FAE;△EAF;GF;
(2)EF=BF+DE.
理由:如图2所示;将△ADE顺时针旋转90°得到△ABG.
由旋转可得:AB=AD,BG=DE,∠1=∠4,∠ABG=∠D=90°,
∴∠ABG+∠ABF=90°+90°=180°,
因此,点G,B,F在同一条直线上.
∵∠FAE=$\frac{1}{2}$∠DAB,
∴∠1+∠5=$\frac{1}{2}$∠DAB.
∴∠4+∠5=∠GAF=$\frac{1}{2}$∠DAB.
∴∠GAF=∠AEF.
∵在△AGF和△AEF中,$\left\{\begin{array}{l}{AG=AE}\\{∠GAF=∠EAF}\\{AF=AF}\end{array}\right.$,
∴△GAF≌△EAF.
∴GF=EF.
∵BG+BF=FG,BG=DE,
∴DE+BF=EF.
(3)当∠B与∠D满足∠B+∠D=180°时,可使得DE+BF=EF.
理由:如图③所示;将△ADE旋转得到△ABG.
由旋转的性质可知:AD=AB、AE=AG,∠DAE=∠BAG.
∵∠ABC+∠D=180°,
∴∠ABG+∠ABC=180°.
∴点G、B、F在一条直线上.
∵∠FAE=$\frac{1}{2}$∠DAB,
∴∠DAE+∠BAF=$\frac{1}{2}$∠DAB.
∴∠GAB+∠BAF=∠GAF=$\frac{1}{2}$∠DAB.
∴∠GAF=∠AEF.
∵在△AGF和△AEF中,$\left\{\begin{array}{l}{AG=AE}\\{∠GAF=∠EAF}\\{AF=AF}\end{array}\right.$,
∴△GAF≌△EAF.
∴GF=EF.
∵BG+BF=FG,BG=DE,
∴DE+BF=EF.
点评 此题主要考查了全等三角形的判定和性质、以及折叠的性质和旋转变换性质等知识,证得△GAF≌△EAF是解题的关键.

 能考试全能100分系列答案
能考试全能100分系列答案| A. | $(a-2)\sqrt{\frac{a^2}{2-a}}=\sqrt{{a^2}(2-a)}$ | B. | $(a-2)\sqrt{\frac{a^2}{2-a}}=\sqrt{a^2}$ | ||
| C. | $(a-2)\sqrt{\frac{a^2}{2-a}}=-\sqrt{{a^2}(2-a)}$ | D. | $(a-2)\sqrt{\frac{a^2}{2-a}}=-\sqrt{a^2}$ |
| A. | 9 | B. | 8 | C. | 2 | D. | 3 |
| A. | (2a-3b)(3b-2a) | B. | (-2a+3b)(2a+3b) | C. | (-2a+3b)(2a-3b) | D. | (2a+3b)(-2a-3b) |
 如图,在Rt△ABC中,∠ACB=90°,∠BAC的平分线交BC于点O,OC=1,以点O为圆心OC为半径作半圆.
如图,在Rt△ABC中,∠ACB=90°,∠BAC的平分线交BC于点O,OC=1,以点O为圆心OC为半径作半圆. 如图,在Rt△ABC中,∠BAC=90°,AB=4,AC=3,点D为BC的中点,动点P从点A出发,以每秒1个单位长度的速度沿线段AB向点B运动,当点P离开点A后,过点P作PE⊥AB交BC于点E,过点E作EF⊥AC于F,设点P运动时间为t(秒),矩形PEFA与△ADE重叠部分的面积为S平方单位长度.
如图,在Rt△ABC中,∠BAC=90°,AB=4,AC=3,点D为BC的中点,动点P从点A出发,以每秒1个单位长度的速度沿线段AB向点B运动,当点P离开点A后,过点P作PE⊥AB交BC于点E,过点E作EF⊥AC于F,设点P运动时间为t(秒),矩形PEFA与△ADE重叠部分的面积为S平方单位长度.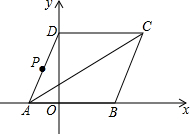 如图所示,菱形ABCD的顶点A、B在x轴上,点A在点B的左侧,点D在y轴的正半轴上,∠BAD=60°.点A的坐标为(-2,0).
如图所示,菱形ABCD的顶点A、B在x轴上,点A在点B的左侧,点D在y轴的正半轴上,∠BAD=60°.点A的坐标为(-2,0).