题目内容
11.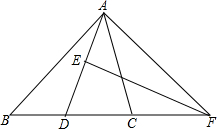 已知:如图所示,在△ABC中,AD平分∠BAC,AD的垂直平分线交AD于E,交BC的延长线于F.求证:∠B=∠CAF.
已知:如图所示,在△ABC中,AD平分∠BAC,AD的垂直平分线交AD于E,交BC的延长线于F.求证:∠B=∠CAF.
分析 根据线段的垂直平分线的性质证明FA=FD,得到∠FAD=∠FDA,根据三角形的外角的性质得到∠FDA=∠B+∠BAD,∠FAD=∠FAC+∠CAD,根据等量代换得到答案.
解答 证明:∵EF是AD的垂直平分线,
∴FA=FD,
∴∠FAD=∠FDA,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵∠FDA=∠B+∠BAD,∠FAD=∠FAC+∠CAD,
∴∠B=∠CAF.
点评 本题考查的是线段的垂直平分线的性质、角平分线的定义和三角形的外角的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
20.若等腰三角形腰长为10cm,底边长为16cm,那么它的面积为( )
| A. | 48cm2 | B. | 36cm2 | C. | 24cm2 | D. | 12cm2 |
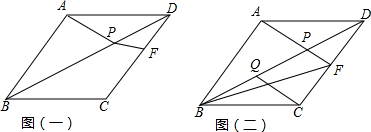
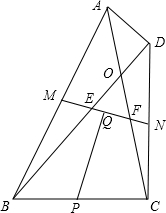 如图,在四边形ABCD中,对角线AC和BD相交于点O,AC=BD,M,P,N分别是边AB,BC,CD的中点,Q是MN的中点.
如图,在四边形ABCD中,对角线AC和BD相交于点O,AC=BD,M,P,N分别是边AB,BC,CD的中点,Q是MN的中点. 已知:如图,AC=CD,AB=CE,BC=ED.求证:△ABC≌△CED.
已知:如图,AC=CD,AB=CE,BC=ED.求证:△ABC≌△CED.