题目内容
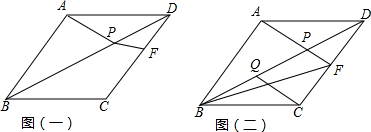
2.如图,△ABD是等腰三角形,AB=AD,将△ABD沿BD翻折至△CBD,过点A作AP⊥AB交BD于点P,点F在线段CD上,(1)如图一,连接PF,若∠DPF=45°,求证:AD=AP+DF
(2)如图二,若∠ABD=30°,点F为AP延长线与CD的交点,点Q在线段BD上,且DQ=3BQ,连接BF、CQ,试探究线段BF与线段CQ的数量关系,并说明理由.
分析 (1)如图(一),连PC,由翻折知:△ABD≌△CBD,根据全等三角形的性质和SAS可证△ABP≌△CBP,根据全等三角形的性质得到AP=CP,∠BCP=∠BAP=90°,设∠2=∠4=α,依此得到CD=CF+FD=PC+FD=AP+DF,即AD=AP+DF;
(2)由翻折知:△CBD≌△ABD,根据全等三角形的性质得到∠DBC=∠BDC=30°,进一步得到DF=$\frac{1}{2}$AD=$\frac{1}{2}$CD,如图(二),作CO⊥BD于O,得到BQ=OQ=$\frac{1}{4}$BD,延长CQ至N,使QN=QC,连NB,根据SAS可证△QNB≌QCO,△NBC≌△FCB,从而得到FB=NC=2QC.
解答 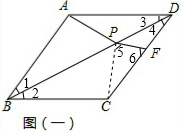 (1)证明:如图(一),连PC,由翻折知:△ABD≌△CBD,
(1)证明:如图(一),连PC,由翻折知:△ABD≌△CBD,
∴AB=BC,∠1=∠2,∠3=∠4,AD=CD,
∵AB=AD,
∴∠1=∠3,
∴∠2=∠4,
在△ABP与△CBP中,
$\left\{\begin{array}{l}{AB=CB}\\{∠1=∠2}\\{BP=BP}\end{array}\right.$,
∴△ABP≌△CBP,
∴AP=CP,∠BCP=∠BAP=90°,
设∠2=∠4=α,
∴∠CPD=∠2+∠BCP=α+90°,
∵∠FPD=45°,
∴∠5=∠CPD-∠FPD=α+90°-45°=α+45°,
∵∠6=∠FPD+∠4=α+45°,
∴∠5=∠6,
∴CP=CF,
∴CD=CF+FD=PC+FD=AP+DF,即AD=AP+DF;
(2)∵AB=AD,∠ABD=30°,
∴∠ADB=∠ABD=30°∠BAD=120°
由翻折知:△CBD≌△ABD,
∴∠DBC=∠BDC=30°,
∵AF⊥BA,
∴∠BAP=90°,
∴∠1=∠BAD-∠BAP=30°,
∵∠ADF=∠ADB+∠BDC=60°,
∴∠AFD=90°,
∴DF=$\frac{1}{2}$AD=$\frac{1}{2}$CD,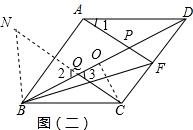 如图(二),作CO⊥BD于O,
如图(二),作CO⊥BD于O,
∵∠BDC=30°,
∴CO=$\frac{1}{2}$CD=DF,
∵CB=CD,CO⊥BD,
∴BO=$\frac{1}{2}$BD,
∵DQ=3BQ,
∴BQ=OQ=$\frac{1}{4}$BD,
延长CQ至N,使QN=QC,连NB,
在△QNB和△QCO中,
$\left\{\begin{array}{l}{QN=QC}\\{∠2=∠3}\\{QB=OQ}\end{array}\right.$,
∴△QNB≌QCO,
∴NB=CO=CF,∠NBQ=∠BOC=90°,
∴∠NBC=∠NBQ+∠DBC=120°=∠BCF,
在△GBC和△FCB中,
$\left\{\begin{array}{l}{NB=FC}\\{∠NBC=∠FCB}\\{BC=BC}\end{array}\right.$,
∴△NBC≌△FCB,
∴FB=NC=2QC.
点评 考查了翻折变换(折叠问题),等腰三角形的性质和全等三角形的判定与性质,本题关键是根据SAS证得△ABP≌△CBP,△QNB≌QCO,△NBC≌△FCB.

 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案| 种植户 | 苹果种植面积(亩) | 梨种植面积(亩) | 出售水果总收入(元) |
| 甲 | 5 | 3 | 33500 |
| 乙 | 3 | 7 | 43500 |
(2)老王、老李计划合租30亩地用来种植苹果和梨,根据市场调查,要求苹果的种植面积大于梨的种植面积(两种水果的种植面积均为整数亩),政府对种植苹果的种植户给予补贴,种植苹果的面积不超过15亩的部分,每亩补贴100元;超过15亩但不超过20亩的部分,每亩补贴200元;超过20亩的部分每亩补贴300元,为了使总收入不低于127500元,则他们有哪几种种植方案?
 在某次军事夏令营射击考核中,甲、乙两名同学各进行了5次射击,射击成绩如图所示,则这两人中水平发挥较为稳定的是甲同学.
在某次军事夏令营射击考核中,甲、乙两名同学各进行了5次射击,射击成绩如图所示,则这两人中水平发挥较为稳定的是甲同学.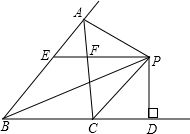 如图,△ABC中,∠ABC的平分线与∠ACB的外角的平分线相交于点P,过点P作BC的平行线交AB,AC分别于点E,F,作PD⊥BC于点D.给出下列三个结论:
如图,△ABC中,∠ABC的平分线与∠ACB的外角的平分线相交于点P,过点P作BC的平行线交AB,AC分别于点E,F,作PD⊥BC于点D.给出下列三个结论: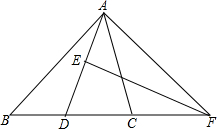 已知:如图所示,在△ABC中,AD平分∠BAC,AD的垂直平分线交AD于E,交BC的延长线于F.求证:∠B=∠CAF.
已知:如图所示,在△ABC中,AD平分∠BAC,AD的垂直平分线交AD于E,交BC的延长线于F.求证:∠B=∠CAF.