题目内容
14.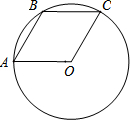 已知A,B,C是⊙O上的三个点,四边形OABC是平行四边形,那么下列结论中错误的是( )
已知A,B,C是⊙O上的三个点,四边形OABC是平行四边形,那么下列结论中错误的是( )| A. | ∠AOC=120° | |
| B. | 四边形OABC一定是菱形 | |
| C. | 若连接AC,则AC=$\sqrt{2}$OA | |
| D. | 若连接AC、BO,则AC与BO互相垂直平分 |
分析 连接OB,AC,根据已知条件得到四边形OABC一定是菱形,根据菱形的性质得到AC与BO互相垂直平分,根据等边三角形的性质得到∠BCO=60°,解直角三角形即可得到结论.
解答 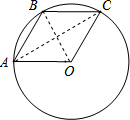 解:连接OB,AC,
解:连接OB,AC,
∵四边形OABC是平行四边形,
∵OA=OC,
∴四边形OABC一定是菱形,
∴则AC与BO互相垂直平分,
∵OB=OC,
∴△BCO是等边三角形,
∴∠BCO=60°,
∴∠AOC=120°,
∵∠OAC=30°,
∴$\frac{1}{2}$AC=$\frac{\sqrt{3}}{2}$OA,
∴AC=$\sqrt{3}$OA.
故选C.
点评 本题考查了圆周角定理,菱形的判定和性质,解直角三角形,熟练掌握菱形的性质是解题的关键.

练习册系列答案
相关题目
9.在同一直角坐标系中,函数y=$-\frac{2}{x}$与y=2x图象的交点个数为( )
| A. | 3 | B. | 1 | C. | 0 | D. | 2 |
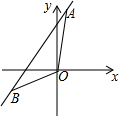 如图,直线a经过点A(1,6),和点B(-3,-2).
如图,直线a经过点A(1,6),和点B(-3,-2). 如图,平行四边形ABCD的对角线交于点O,且AB=5,△OCD的周长为23,则平行四边形ABCD的两条对角线的和是36.
如图,平行四边形ABCD的对角线交于点O,且AB=5,△OCD的周长为23,则平行四边形ABCD的两条对角线的和是36.