题目内容
5.计算:(1)$\sqrt{12}$($\sqrt{75}$+3$\sqrt{\frac{1}{3}}$-$\sqrt{48}$)
(2)(7+4$\sqrt{3}$)(7-4$\sqrt{3}$)-(2$\sqrt{5}$-1)2.
分析 (1)先化简,合并后再进一步计算乘法即可;
(2)利用平方差公式和完全平方公式计算,进一步合并得出答案即可.
解答 解:(1)原式=2$\sqrt{3}$(5$\sqrt{3}$+$\sqrt{3}$-4$\sqrt{3}$)
=2$\sqrt{3}$×2$\sqrt{3}$
=12;
(2)原式=49-48-(20-4$\sqrt{5}$+1)
=1+4$\sqrt{5}$-21
=4$\sqrt{5}$-20.
点评 此题考查二次根式的混合运算,掌握二次根式的化简方法、计算方法与合并方法是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.如图,直线a与b相交于点O,MO⊥直线a,垂足为O,若∠2=35°,则∠1的度数为( )


| A. | 75° | B. | 65° | C. | 60° | D. | 55° |
20.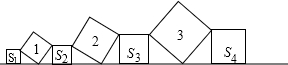 如图,直线l上依次摆放着一系列正方形,斜放置的正方形面积分别为1,2,3,…,n,正放置的正方形面积分别为S1,S2,S3,…,Sn,当n=100时,则S1+S2+S3+…+S100等于( )
如图,直线l上依次摆放着一系列正方形,斜放置的正方形面积分别为1,2,3,…,n,正放置的正方形面积分别为S1,S2,S3,…,Sn,当n=100时,则S1+S2+S3+…+S100等于( )
 如图,直线l上依次摆放着一系列正方形,斜放置的正方形面积分别为1,2,3,…,n,正放置的正方形面积分别为S1,S2,S3,…,Sn,当n=100时,则S1+S2+S3+…+S100等于( )
如图,直线l上依次摆放着一系列正方形,斜放置的正方形面积分别为1,2,3,…,n,正放置的正方形面积分别为S1,S2,S3,…,Sn,当n=100时,则S1+S2+S3+…+S100等于( )| A. | 2500 | B. | 2550 | C. | 2600 | D. | 2800 |
14.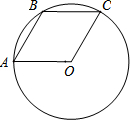 已知A,B,C是⊙O上的三个点,四边形OABC是平行四边形,那么下列结论中错误的是( )
已知A,B,C是⊙O上的三个点,四边形OABC是平行四边形,那么下列结论中错误的是( )
 已知A,B,C是⊙O上的三个点,四边形OABC是平行四边形,那么下列结论中错误的是( )
已知A,B,C是⊙O上的三个点,四边形OABC是平行四边形,那么下列结论中错误的是( )| A. | ∠AOC=120° | |
| B. | 四边形OABC一定是菱形 | |
| C. | 若连接AC,则AC=$\sqrt{2}$OA | |
| D. | 若连接AC、BO,则AC与BO互相垂直平分 |
 如图,在矩形ABCD中,对角线AC、BD交于点O,若∠AOD=120°,AB=1,则矩形ABCD的面积=$\sqrt{3}$.
如图,在矩形ABCD中,对角线AC、BD交于点O,若∠AOD=120°,AB=1,则矩形ABCD的面积=$\sqrt{3}$.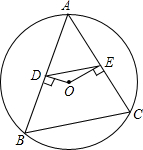 如图所示,△ABC为⊙O的内接三角形,点O为圆心,OD⊥AB,垂足为D,OE⊥AC,垂足为E,若DE=3,则BC=6.
如图所示,△ABC为⊙O的内接三角形,点O为圆心,OD⊥AB,垂足为D,OE⊥AC,垂足为E,若DE=3,则BC=6.