题目内容
9.在同一直角坐标系中,函数y=$-\frac{2}{x}$与y=2x图象的交点个数为( )| A. | 3 | B. | 1 | C. | 0 | D. | 2 |
分析 本题只需结合函数的图象联立两方程进行求解,根据解的个数即可判断交点的个数.
解答 解:依题意有$\left\{\begin{array}{l}{y=-\frac{2}{x}}\\{y=2x}\end{array}\right.$,
解得x2=-1,x无解,
故两函数没有交点.
故选C.
点评 本题考查了反比例函数与一次函数的交点问题,也可以通过画两条函数的图象,没有交点,即交点为0.

练习册系列答案
相关题目
20.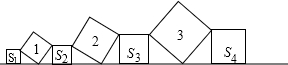 如图,直线l上依次摆放着一系列正方形,斜放置的正方形面积分别为1,2,3,…,n,正放置的正方形面积分别为S1,S2,S3,…,Sn,当n=100时,则S1+S2+S3+…+S100等于( )
如图,直线l上依次摆放着一系列正方形,斜放置的正方形面积分别为1,2,3,…,n,正放置的正方形面积分别为S1,S2,S3,…,Sn,当n=100时,则S1+S2+S3+…+S100等于( )
 如图,直线l上依次摆放着一系列正方形,斜放置的正方形面积分别为1,2,3,…,n,正放置的正方形面积分别为S1,S2,S3,…,Sn,当n=100时,则S1+S2+S3+…+S100等于( )
如图,直线l上依次摆放着一系列正方形,斜放置的正方形面积分别为1,2,3,…,n,正放置的正方形面积分别为S1,S2,S3,…,Sn,当n=100时,则S1+S2+S3+…+S100等于( )| A. | 2500 | B. | 2550 | C. | 2600 | D. | 2800 |
4. 如图,矩形ABCD的边AB上有一点P,且AD=$\frac{5}{3}$,BP=$\frac{4}{5}$.以点P为直角顶点的直角三角形两条直角边分别交线段DC,线段BC于点E,F,连接EF,则tan∠PEF的值( )
如图,矩形ABCD的边AB上有一点P,且AD=$\frac{5}{3}$,BP=$\frac{4}{5}$.以点P为直角顶点的直角三角形两条直角边分别交线段DC,线段BC于点E,F,连接EF,则tan∠PEF的值( )
 如图,矩形ABCD的边AB上有一点P,且AD=$\frac{5}{3}$,BP=$\frac{4}{5}$.以点P为直角顶点的直角三角形两条直角边分别交线段DC,线段BC于点E,F,连接EF,则tan∠PEF的值( )
如图,矩形ABCD的边AB上有一点P,且AD=$\frac{5}{3}$,BP=$\frac{4}{5}$.以点P为直角顶点的直角三角形两条直角边分别交线段DC,线段BC于点E,F,连接EF,则tan∠PEF的值( )| A. | $\frac{12}{25}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{3}{5}$ |
14.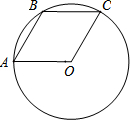 已知A,B,C是⊙O上的三个点,四边形OABC是平行四边形,那么下列结论中错误的是( )
已知A,B,C是⊙O上的三个点,四边形OABC是平行四边形,那么下列结论中错误的是( )
 已知A,B,C是⊙O上的三个点,四边形OABC是平行四边形,那么下列结论中错误的是( )
已知A,B,C是⊙O上的三个点,四边形OABC是平行四边形,那么下列结论中错误的是( )| A. | ∠AOC=120° | |
| B. | 四边形OABC一定是菱形 | |
| C. | 若连接AC,则AC=$\sqrt{2}$OA | |
| D. | 若连接AC、BO,则AC与BO互相垂直平分 |
18. 如图所示,是六个棱长为1的立方块组成的一个几何体,其左视图的面积是( )
如图所示,是六个棱长为1的立方块组成的一个几何体,其左视图的面积是( )
 如图所示,是六个棱长为1的立方块组成的一个几何体,其左视图的面积是( )
如图所示,是六个棱长为1的立方块组成的一个几何体,其左视图的面积是( )| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
19.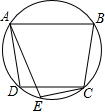 如图,在⊙O中,AB∥CD,∠BCD=100°,E为$\widehat{DC}$上的任意一点,A、B、C、D是⊙O上的四个点,则∠AEC的角度为( )
如图,在⊙O中,AB∥CD,∠BCD=100°,E为$\widehat{DC}$上的任意一点,A、B、C、D是⊙O上的四个点,则∠AEC的角度为( )
 如图,在⊙O中,AB∥CD,∠BCD=100°,E为$\widehat{DC}$上的任意一点,A、B、C、D是⊙O上的四个点,则∠AEC的角度为( )
如图,在⊙O中,AB∥CD,∠BCD=100°,E为$\widehat{DC}$上的任意一点,A、B、C、D是⊙O上的四个点,则∠AEC的角度为( )| A. | 110° | B. | 70° | C. | 80° | D. | 100° |
 某农户用5$\sqrt{11}$米长的围栏围出一块如图所示的长方形土地(墙面是长方形土地的长),已知该长方形土地的宽为$\frac{3\sqrt{11}}{2}$米,则该长方形土地的周长为7$\sqrt{11}$米.
某农户用5$\sqrt{11}$米长的围栏围出一块如图所示的长方形土地(墙面是长方形土地的长),已知该长方形土地的宽为$\frac{3\sqrt{11}}{2}$米,则该长方形土地的周长为7$\sqrt{11}$米.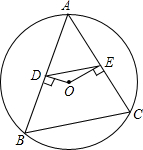 如图所示,△ABC为⊙O的内接三角形,点O为圆心,OD⊥AB,垂足为D,OE⊥AC,垂足为E,若DE=3,则BC=6.
如图所示,△ABC为⊙O的内接三角形,点O为圆心,OD⊥AB,垂足为D,OE⊥AC,垂足为E,若DE=3,则BC=6.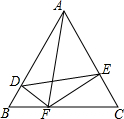 如图,△ABC是边长为a的等边三角形,DF⊥AB,EF⊥AC.
如图,△ABC是边长为a的等边三角形,DF⊥AB,EF⊥AC.