题目内容
19. 如图,平行四边形ABCD的对角线交于点O,且AB=5,△OCD的周长为23,则平行四边形ABCD的两条对角线的和是36.
如图,平行四边形ABCD的对角线交于点O,且AB=5,△OCD的周长为23,则平行四边形ABCD的两条对角线的和是36.
分析 根据平行四边形的性质可得CD=AB=5,DO=BO,CO=AO,再由△OCD的周长为23可得DO+CO=18,进而可得AC+BD=2(DO+CO)=36.
解答 解:∵四边形ABCD是平行四边形,
∴CD=AB,DO=BO,CO=AO,
∵AB=5,
∴CD=5,
∵△OCD的周长为23,
∴DO+CO=18,
∴AC+BD=36,
故答案为:36.
点评 此题主要考查了平行四边形的性质,关键是掌握平行四边形的性质:①边:平行四边形的对边相等.②角:平行四边形的对角相等.③对角线:平行四边形的对角线互相平分.

练习册系列答案
相关题目
14.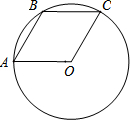 已知A,B,C是⊙O上的三个点,四边形OABC是平行四边形,那么下列结论中错误的是( )
已知A,B,C是⊙O上的三个点,四边形OABC是平行四边形,那么下列结论中错误的是( )
 已知A,B,C是⊙O上的三个点,四边形OABC是平行四边形,那么下列结论中错误的是( )
已知A,B,C是⊙O上的三个点,四边形OABC是平行四边形,那么下列结论中错误的是( )| A. | ∠AOC=120° | |
| B. | 四边形OABC一定是菱形 | |
| C. | 若连接AC,则AC=$\sqrt{2}$OA | |
| D. | 若连接AC、BO,则AC与BO互相垂直平分 |
4.下列数:-3,1,-2,0中,最小的是( )
| A. | -3 | B. | 0 | C. | -2 | D. | 1 |
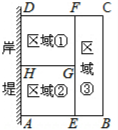 为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为80m的围网在水库中围成了如图所示的①②③三块长方形区域,而且这三块长方形区域的面积相等.设BC的长度为xm,AB为ym.
为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为80m的围网在水库中围成了如图所示的①②③三块长方形区域,而且这三块长方形区域的面积相等.设BC的长度为xm,AB为ym.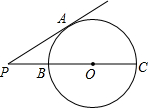 如图,PA切⊙O于点A,PC过点O且交⊙O于点B,C,若PA=2$\sqrt{3}$,PB=2,则⊙O的半径为2.
如图,PA切⊙O于点A,PC过点O且交⊙O于点B,C,若PA=2$\sqrt{3}$,PB=2,则⊙O的半径为2. 我军某部队上午9时在南海巡航,某军舰位于南海的A处,观察到一小岛P位于军舰的北偏西67.5°,军舰以21海里/时的速度向正北方向行驶,下午2时军舰到达B处,这时观测到城市P位于军舰的南偏西36.9°方向,求此时军舰所在B处与城市P的距离?(参考数据:sin36.9°≈$\frac{3}{5}$,tan36.9°≈$\frac{3}{4}$,sin67.5°≈$\frac{12}{13}$,tan67.5°≈$\frac{12}{5}$)
我军某部队上午9时在南海巡航,某军舰位于南海的A处,观察到一小岛P位于军舰的北偏西67.5°,军舰以21海里/时的速度向正北方向行驶,下午2时军舰到达B处,这时观测到城市P位于军舰的南偏西36.9°方向,求此时军舰所在B处与城市P的距离?(参考数据:sin36.9°≈$\frac{3}{5}$,tan36.9°≈$\frac{3}{4}$,sin67.5°≈$\frac{12}{13}$,tan67.5°≈$\frac{12}{5}$)