题目内容
6.(1)计算:(-2015)0+$\root{3}{8}$-${({-\frac{1}{2}})^{-1}}$+2cos45°;(2)先化简,再求值:1-$\frac{a-b}{a+2b}÷\frac{{{a^2}-{b^2}}}{{{a^2}+4ab+4{b^2}}}$,其中a=1,b=-2.
分析 (1)根据零指数幂、负整数指数幂、特殊角的三角函数值可以解答本题;
(2)先对原式化简,再将a=1,b=-2代入化简后的式子即可解答本题.
解答 (1)解:原式=1+2-(-2)+2×$\frac{\sqrt{2}}{2}$
=1+2+2+$\sqrt{2}$
=5+$\sqrt{2}$;
(2)解:原式=$1-\frac{a-b}{a+2b}•\frac{{{{({a+2b})}^2}}}{{({a+b})({a-b})}}$
=$1-\frac{{a+2{b^{\;}}}}{a+b}$
=$\frac{a+b-a-2b}{a+b}$
=$-\frac{b}{a+b}$
当a=1,b=-2时,
原式=$-\frac{-2}{1-2}=-2$.
点评 本题考查分式的化简求值、负整数指数幂、实数的运算、零指数幂、特殊角的三角函数值,解题的关键是明确它们各自的含义,可以对原式化简求值.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
16.如图,直线a与b相交于点O,MO⊥直线a,垂足为O,若∠2=35°,则∠1的度数为( )


| A. | 75° | B. | 65° | C. | 60° | D. | 55° |
14.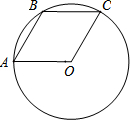 已知A,B,C是⊙O上的三个点,四边形OABC是平行四边形,那么下列结论中错误的是( )
已知A,B,C是⊙O上的三个点,四边形OABC是平行四边形,那么下列结论中错误的是( )
 已知A,B,C是⊙O上的三个点,四边形OABC是平行四边形,那么下列结论中错误的是( )
已知A,B,C是⊙O上的三个点,四边形OABC是平行四边形,那么下列结论中错误的是( )| A. | ∠AOC=120° | |
| B. | 四边形OABC一定是菱形 | |
| C. | 若连接AC,则AC=$\sqrt{2}$OA | |
| D. | 若连接AC、BO,则AC与BO互相垂直平分 |
18. 如图所示,是六个棱长为1的立方块组成的一个几何体,其左视图的面积是( )
如图所示,是六个棱长为1的立方块组成的一个几何体,其左视图的面积是( )
 如图所示,是六个棱长为1的立方块组成的一个几何体,其左视图的面积是( )
如图所示,是六个棱长为1的立方块组成的一个几何体,其左视图的面积是( )| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
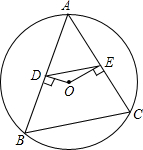 如图所示,△ABC为⊙O的内接三角形,点O为圆心,OD⊥AB,垂足为D,OE⊥AC,垂足为E,若DE=3,则BC=6.
如图所示,△ABC为⊙O的内接三角形,点O为圆心,OD⊥AB,垂足为D,OE⊥AC,垂足为E,若DE=3,则BC=6.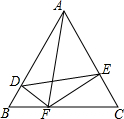 如图,△ABC是边长为a的等边三角形,DF⊥AB,EF⊥AC.
如图,△ABC是边长为a的等边三角形,DF⊥AB,EF⊥AC.