题目内容
4．$\sqrt{12}×2cos30°$+|-2|-（-$\frac{1}{3}$）-1．分析 原式第一项利用二次根式性质及特殊角的三角函数值化简，第二项利用绝对值的代数意义化简，最后一项利用负整数指数幂法则计算即可得到结果．
解答 解：原式=2$\sqrt{3}$×2×$\frac{\sqrt{3}}{2}$+2+3
=6+2+3
=11．
点评 此题考查了实数的运算，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
14．
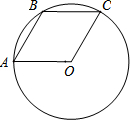已知A，B，C是⊙O上的三个点，四边形OABC是平行四边形，那么下列结论中错误的是（ ）
已知A，B，C是⊙O上的三个点，四边形OABC是平行四边形，那么下列结论中错误的是（ ）| A． | ∠AOC=120° | |
| B． | 四边形OABC一定是菱形 | |
| C． | 若连接AC，则AC=$\sqrt{2}$OA | |
| D． | 若连接AC、BO，则AC与BO互相垂直平分 |
12．
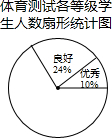某市为了解中学生参加体育训练的情况，组织部分学生参加测试进行抽样调查，其过程如下：
从全市抽取2000名学生进行体育测试：
①从某所初中学校抽取2000名学生；
②从全市九年级学生中随机抽取2000名学生；
③从全市初中生中随机抽取2000名学生．
其中你认为合理的抽样方法为③（填数学序号）
整理数据：
对测试结果进行整理，分为四个等级：优秀；良好；及格；不及格，并将测试结果绘成了如图两幅不完整的统计图．请补全频数分布表和扇形统计图：
分析数据：
若该市共有3万名初中学生，根据测试情况请你估计不及格的人数有多少？
针对本次测试得到的相关信息，你有何看法和建议？（字数不超过30字）
某市为了解中学生参加体育训练的情况，组织部分学生参加测试进行抽样调查，其过程如下：从全市抽取2000名学生进行体育测试：
①从某所初中学校抽取2000名学生；
②从全市九年级学生中随机抽取2000名学生；
③从全市初中生中随机抽取2000名学生．
其中你认为合理的抽样方法为③（填数学序号）
整理数据：
对测试结果进行整理，分为四个等级：优秀；良好；及格；不及格，并将测试结果绘成了如图两幅不完整的统计图．请补全频数分布表和扇形统计图：
| 测试结果 | 频数 | 频率 |
| 优秀 | 200 | 0.1 |
| 良好 | 480 | 0.24 |
| 及格 | 1020 | 0.51 |
| 不及格 | 300 | 0.15 |
若该市共有3万名初中学生，根据测试情况请你估计不及格的人数有多少？
针对本次测试得到的相关信息，你有何看法和建议？（字数不超过30字）
19．
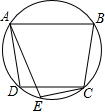如图，在⊙O中，AB∥CD，∠BCD=100°，E为$\widehat{DC}$上的任意一点，A、B、C、D是⊙O上的四个点，则∠AEC的角度为（ ）
如图，在⊙O中，AB∥CD，∠BCD=100°，E为$\widehat{DC}$上的任意一点，A、B、C、D是⊙O上的四个点，则∠AEC的角度为（ ）| A． | 110° | B． | 70° | C． | 80° | D． | 100° |
我军某部队上午9时在南海巡航，某军舰位于南海的A处，观察到一小岛P位于军舰的北偏西67.5°，军舰以21海里/时的速度向正北方向行驶，下午2时军舰到达B处，这时观测到城市P位于军舰的南偏西36.9°方向，求此时军舰所在B处与城市P的距离？（参考数据：sin36.9°≈$\frac{3}{5}$，tan36.9°≈$\frac{3}{4}$，sin67.5°≈$\frac{12}{13}$，tan67.5°≈$\frac{12}{5}$）
13．为提高饮水质量，越来越多的居民选购家用净水器，一商场抓住商机，从厂家购进了A，B两种型号家用净水器，其数量和进价如表：
为使每台B型号家用净水器的售价是A型号的2倍，且保证售完这批家用净水器的利润不低于1650元，每台A型号家用净水器的售价至少应为多少元？（注：利润=售价-进价）
| 型号 | 数量（台） | 进价（元/台） |
| A | 10 | 150元 |
| B | 5 | 350元 |
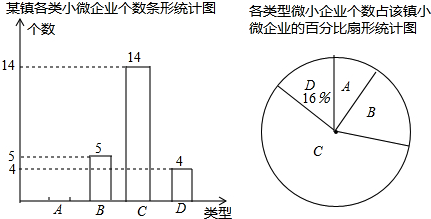
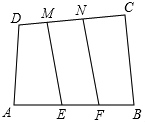挑战极限：如图，已知四边形ABCD的面积为S，E、F为AB的三等分点，M、N为DC的三等分点．四边形EFNM的面积=$\frac{1}{3}$S．（选填“＞”，“＜”，“=”，“≤”，“≥”）