题目内容
2.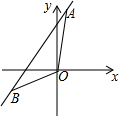 如图,直线a经过点A(1,6),和点B(-3,-2).
如图,直线a经过点A(1,6),和点B(-3,-2).(1)求直线a的解析式;
(2)求直线与坐标轴的交点坐标;
(3)求S△AOB.
分析 (1)设直线a的解析式为y=kx+b,用待定系数法求一次函数的解析式即可;
(2)令x=0和y=0得出直线与坐标轴的交点坐标;
(3)设直线a与有轴交于点C,根据S△AOB=S△AOC+S△COB得出答案即可.
解答 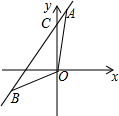 解:(1)设直线a的解析式为y=kx+b,
解:(1)设直线a的解析式为y=kx+b,
∵直线a经过点A(1,6),和点B(-3,-2),
∴$\left\{\begin{array}{l}{k+b=6}\\{-3k+b=-2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=2}\\{b=4}\end{array}\right.$,
∴直线a的解析式为y=2x+4;
(2)令x=0,得y=4;
令y=0得x=-2,
∴直线与坐标轴的交点坐标(-2,0)(0,4);
(3)设直线a与y轴交于点C,
∴S△AOB=S△AOC+S△COB=$\frac{1}{2}$×4×3+$\frac{1}{2}$×4×1=8.
点评 本题考查了待定系数法求一次函数解析式以及三角形面积求法,根据已知得出函数解析式是解题关键.

练习册系列答案
相关题目
14.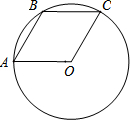 已知A,B,C是⊙O上的三个点,四边形OABC是平行四边形,那么下列结论中错误的是( )
已知A,B,C是⊙O上的三个点,四边形OABC是平行四边形,那么下列结论中错误的是( )
 已知A,B,C是⊙O上的三个点,四边形OABC是平行四边形,那么下列结论中错误的是( )
已知A,B,C是⊙O上的三个点,四边形OABC是平行四边形,那么下列结论中错误的是( )| A. | ∠AOC=120° | |
| B. | 四边形OABC一定是菱形 | |
| C. | 若连接AC,则AC=$\sqrt{2}$OA | |
| D. | 若连接AC、BO,则AC与BO互相垂直平分 |
12. 某市为了解中学生参加体育训练的情况,组织部分学生参加测试进行抽样调查,其过程如下:
某市为了解中学生参加体育训练的情况,组织部分学生参加测试进行抽样调查,其过程如下:
从全市抽取2000名学生进行体育测试:
①从某所初中学校抽取2000名学生;
②从全市九年级学生中随机抽取2000名学生;
③从全市初中生中随机抽取2000名学生.
其中你认为合理的抽样方法为③(填数学序号)
整理数据:
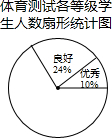
对测试结果进行整理,分为四个等级:优秀;良好;及格;不及格,并将测试结果绘成了如图两幅不完整的统计图.请补全频数分布表和扇形统计图:
分析数据:
若该市共有3万名初中学生,根据测试情况请你估计不及格的人数有多少?
针对本次测试得到的相关信息,你有何看法和建议?(字数不超过30字)
 某市为了解中学生参加体育训练的情况,组织部分学生参加测试进行抽样调查,其过程如下:
某市为了解中学生参加体育训练的情况,组织部分学生参加测试进行抽样调查,其过程如下:从全市抽取2000名学生进行体育测试:
①从某所初中学校抽取2000名学生;
②从全市九年级学生中随机抽取2000名学生;
③从全市初中生中随机抽取2000名学生.
其中你认为合理的抽样方法为③(填数学序号)
整理数据:
对测试结果进行整理,分为四个等级:优秀;良好;及格;不及格,并将测试结果绘成了如图两幅不完整的统计图.请补全频数分布表和扇形统计图:
| 测试结果 | 频数 | 频率 |
| 优秀 | 200 | 0.1 |
| 良好 | 480 | 0.24 |
| 及格 | 1020 | 0.51 |
| 不及格 | 300 | 0.15 |
若该市共有3万名初中学生,根据测试情况请你估计不及格的人数有多少?
针对本次测试得到的相关信息,你有何看法和建议?(字数不超过30字)
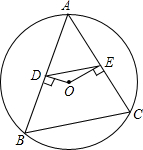 如图所示,△ABC为⊙O的内接三角形,点O为圆心,OD⊥AB,垂足为D,OE⊥AC,垂足为E,若DE=3,则BC=6.
如图所示,△ABC为⊙O的内接三角形,点O为圆心,OD⊥AB,垂足为D,OE⊥AC,垂足为E,若DE=3,则BC=6.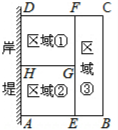 为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为80m的围网在水库中围成了如图所示的①②③三块长方形区域,而且这三块长方形区域的面积相等.设BC的长度为xm,AB为ym.
为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为80m的围网在水库中围成了如图所示的①②③三块长方形区域,而且这三块长方形区域的面积相等.设BC的长度为xm,AB为ym.