题目内容
6. 如图,OE是∠AOB的平分线,CD∥OB交OE于点D,∠ACD=50°,则∠CDE的度数为( )
如图,OE是∠AOB的平分线,CD∥OB交OE于点D,∠ACD=50°,则∠CDE的度数为( )| A. | 125° | B. | 130° | C. | 140° | D. | 155° |
分析 先利用平行线的性质得∠AOB=∠ACD=50°,再根据角平分线定义得∠AOE=$\frac{1}{2}$∠AOB=25°,根据邻补角定义得∠OCD=180°-∠ACD=130°,然后根据三角形外角性质计算∠CDE的度数.
解答 解:∵CD∥OB,
∴∠AOB=∠ACD=50°,
∵OE是∠AOB的平分线,
∴∠AOE=$\frac{1}{2}$∠AOB=25°,
∵∠OCD=180°-∠ACD=130°,
∴∠CDE=∠OCD+∠COD=130°+25°=155°.
故选D.
点评 本题考查了平行线性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.

练习册系列答案
相关题目
14.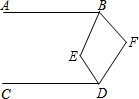 如图,已知AB∥CD,∠EBF=2∠ABE,∠EDF=2∠CDE,则∠E与∠F之间满足的数量关系是( )
如图,已知AB∥CD,∠EBF=2∠ABE,∠EDF=2∠CDE,则∠E与∠F之间满足的数量关系是( )
 如图,已知AB∥CD,∠EBF=2∠ABE,∠EDF=2∠CDE,则∠E与∠F之间满足的数量关系是( )
如图,已知AB∥CD,∠EBF=2∠ABE,∠EDF=2∠CDE,则∠E与∠F之间满足的数量关系是( )| A. | ∠E=∠F | B. | ∠E+∠F=180° | C. | 3∠E+∠F=360° | D. | 2∠E-∠F=90° |
18.下列四个命题中是真命题的是( )
| A. | 相等的角是对顶角 | |
| B. | 两条直线被第三条直线所截,同位角相等 | |
| C. | 实数与数轴上的点是一一对应的 | |
| D. | 如果一个数能被2整除,那么它也能被4整除 |
15.用小数表示3.56×10-7为( )
| A. | 0.000000356 | B. | 0.0000000356 | C. | 0.00000000356 | D. | 0.000000000356 |
16. 如图所示是由四根木棒搭成的平行四边形框架,AB=8cm,AD=6cm,在此位置上,使AB固定,逆时针转动AD.则关于?ABCD面积变化情况叙述正确的是( )
如图所示是由四根木棒搭成的平行四边形框架,AB=8cm,AD=6cm,在此位置上,使AB固定,逆时针转动AD.则关于?ABCD面积变化情况叙述正确的是( )
 如图所示是由四根木棒搭成的平行四边形框架,AB=8cm,AD=6cm,在此位置上,使AB固定,逆时针转动AD.则关于?ABCD面积变化情况叙述正确的是( )
如图所示是由四根木棒搭成的平行四边形框架,AB=8cm,AD=6cm,在此位置上,使AB固定,逆时针转动AD.则关于?ABCD面积变化情况叙述正确的是( )| A. | 先变大,再变小 | B. | 先变小,再变大 | ||
| C. | 保持不变 | D. | 转动过程中,?ABCD面积没有最大值 |
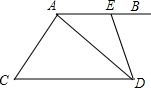 如图,AB∥CD,E为AB上一点,∠BED=2∠BAD.
如图,AB∥CD,E为AB上一点,∠BED=2∠BAD.