题目内容
9. 如图,正方形网格的每个小正方形的边长均为1,每个小正方形的顶点叫做格点,图中四条线段的端点均在格点上.
如图,正方形网格的每个小正方形的边长均为1,每个小正方形的顶点叫做格点,图中四条线段的端点均在格点上.(1)平移图中的线段,你能使哪三条线段首尾连接构成一个格点三角形,请画出平移后的图形;
(2)判断并说明三角形的形状.
分析 (1)把线段②不动,平移③④,使线段②③④首尾连接构成一个三角形;
(2)先利用勾股定理计算出AB、AC、BC,然后利用勾股定理的逆定理可证明△ACB为直角三角形.
解答 解:(1)如图,线段②③④首尾连接构成一个三角形,△ABC为所作;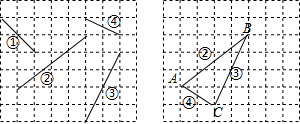
(2)△ABC为直角三角形.理由如下:
∵AC2=12+22=5,BC2=22+42=20,AC2=32+42=25,
而5+20=25,
∴AC2+BC2=AC2,
∴△ACB为直角三角形,∠ACB=90°.
点评 本题考查了作图-平移变换:确定平移后图形的基本要素有两个:平移方向、平移距离.作图时要先找到图形的关键点,分别把这几个关键点按照平移的方向和距离确定对应点后,再顺次连接对应点即可得到平移后的图形.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
19.计算:$\sqrt{9a}$+$\sqrt{25a}$=( )
| A. | 8$\sqrt{a}$ | B. | $\sqrt{34a}$ | C. | 8a | D. | 15$\sqrt{a}$ |
4. 如图,在?ABCD中,BC=10,AC=8,BD=14,则△BOC的周长是( )
如图,在?ABCD中,BC=10,AC=8,BD=14,则△BOC的周长是( )
 如图,在?ABCD中,BC=10,AC=8,BD=14,则△BOC的周长是( )
如图,在?ABCD中,BC=10,AC=8,BD=14,则△BOC的周长是( )| A. | 21 | B. | 22 | C. | 25 | D. | 32 |
14.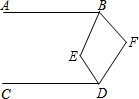 如图,已知AB∥CD,∠EBF=2∠ABE,∠EDF=2∠CDE,则∠E与∠F之间满足的数量关系是( )
如图,已知AB∥CD,∠EBF=2∠ABE,∠EDF=2∠CDE,则∠E与∠F之间满足的数量关系是( )
 如图,已知AB∥CD,∠EBF=2∠ABE,∠EDF=2∠CDE,则∠E与∠F之间满足的数量关系是( )
如图,已知AB∥CD,∠EBF=2∠ABE,∠EDF=2∠CDE,则∠E与∠F之间满足的数量关系是( )| A. | ∠E=∠F | B. | ∠E+∠F=180° | C. | 3∠E+∠F=360° | D. | 2∠E-∠F=90° |
18.下列四个命题中是真命题的是( )
| A. | 相等的角是对顶角 | |
| B. | 两条直线被第三条直线所截,同位角相等 | |
| C. | 实数与数轴上的点是一一对应的 | |
| D. | 如果一个数能被2整除,那么它也能被4整除 |
19. 如图,在平行四边形ABCD中,∠A+∠C=220°,则∠B的度数是( )
如图,在平行四边形ABCD中,∠A+∠C=220°,则∠B的度数是( )
 如图,在平行四边形ABCD中,∠A+∠C=220°,则∠B的度数是( )
如图,在平行四边形ABCD中,∠A+∠C=220°,则∠B的度数是( )| A. | 60° | B. | 70° | C. | 100° | D. | 120° |

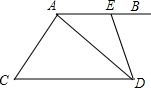 如图,AB∥CD,E为AB上一点,∠BED=2∠BAD.
如图,AB∥CD,E为AB上一点,∠BED=2∠BAD.