题目内容
1.已知abc<0,且a+b+c>0,x=$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$,则代数式x2008-2007x的值为-2006.分析 根据同号得正、异号得负以及有理数的加法运算法则判断出a、b、c三个数中只有一个负数,然后求出x的值,再代入代数式进行计算即可得解.
解答 解:∵abc<0,且a+b+c>0,
∴a、b、c三个数中只有一个负数,两个正数,
不妨设a、b是正数,c是负数,
∴x=$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$=1+1-1=1,
∴x2008-2007x=12008-2007×1=1-2007=-2006.
故答案为:-2006.
点评 本题考查了代数式求值,有理数的乘法和加法运算,熟记运算法则并判断出三个数的正数、负数的个数是解题的关键.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
 如图,点C、E和点B、D、F分别在∠GAH的两边上,且∠A=18°,AB=BC=CD=DE=EF,则∠GEF=90度.
如图,点C、E和点B、D、F分别在∠GAH的两边上,且∠A=18°,AB=BC=CD=DE=EF,则∠GEF=90度.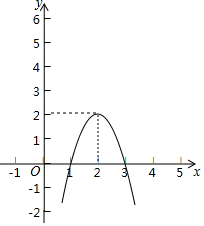 如图,二次函数y=-2(x-2)2+2的图象.
如图,二次函数y=-2(x-2)2+2的图象. 如图是一个长方形推拉窗,窗高1.5米.当活动窗扇拉开长度b(米)时,长方形窗框的通风面积为1.5b米2.
如图是一个长方形推拉窗,窗高1.5米.当活动窗扇拉开长度b(米)时,长方形窗框的通风面积为1.5b米2. 已知:点B、E、C、F在同一直线上,AC=DF,∠A=∠D,AB∥DE.试说明:BE=CF.
已知:点B、E、C、F在同一直线上,AC=DF,∠A=∠D,AB∥DE.试说明:BE=CF. 如图,在△ABC中,∠B=90°,AB=6cm,BC=8cm,动点P从点A开始沿AB边向B以1cm/s的速度移动(不与点B重合);动点Q从B点开始沿BC边向点C以2cm/s的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,出发多少秒后,四边形APQC的面积为16cm2?
如图,在△ABC中,∠B=90°,AB=6cm,BC=8cm,动点P从点A开始沿AB边向B以1cm/s的速度移动(不与点B重合);动点Q从B点开始沿BC边向点C以2cm/s的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,出发多少秒后,四边形APQC的面积为16cm2?