题目内容
11. 如图,点C、E和点B、D、F分别在∠GAH的两边上,且∠A=18°,AB=BC=CD=DE=EF,则∠GEF=90度.
如图,点C、E和点B、D、F分别在∠GAH的两边上,且∠A=18°,AB=BC=CD=DE=EF,则∠GEF=90度.
分析 根据AB=BC=CD=DE=EF利用等腰三角形的性质即可找出各角的度数,再根据三角形外角的性质即可求出结论.
解答 解:∵AB=BC=CD=DE=EF,且∠A=18°,
∴∠ACB=∠A=18°,∠CBD=∠CDB=2∠A=36°,∠DCE=∠DEC=∠A+∠BDC=3∠A=54°,∠EDF=∠EFD=∠A+∠DEC=4∠A=72°,
∴∠FEG=∠A+∠EFD=5∠A=90°.
故答案为:90.
点评 本题考查了等腰三角形的性质以及外角的性质,根据等腰三角形的性质求出各角的度数是解题的关键.

练习册系列答案
相关题目
6.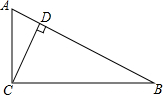 如图,在Rt△ABC中,∠ACB=90°,AC=5cm,BC=12cm,其中斜边上的高为( )
如图,在Rt△ABC中,∠ACB=90°,AC=5cm,BC=12cm,其中斜边上的高为( )
 如图,在Rt△ABC中,∠ACB=90°,AC=5cm,BC=12cm,其中斜边上的高为( )
如图,在Rt△ABC中,∠ACB=90°,AC=5cm,BC=12cm,其中斜边上的高为( )| A. | 6cm | B. | 8.5cm | C. | $\frac{60}{13}$cm | D. | $\frac{30}{13}$cm |
16.已知n是正整数,则下列数中一定能整除(2n+3)2-25的是( )
| A. | 6 | B. | 3 | C. | 4 | D. | 5 |
3.下列算式中,错误的是( )
| A. | a(a+b)+b(a+b)=a2+2ab+b2 | B. | x(x-y)+y(x-y)=x2-y2 | ||
| C. | a(a2-ab+b2)+b(a2-ab+b2)=a3+b3 | D. | x(x-y)-y(x-y)=y2-x2 |
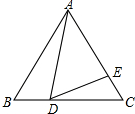 如图所示,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADB+∠EDC=120°,BD=3,CE=2,则△ABC的边长为( )
如图所示,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADB+∠EDC=120°,BD=3,CE=2,则△ABC的边长为( )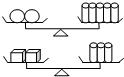 如图所示,第一个天平的两侧分别放2个球体和5个圆柱体,第二个天平的两侧分别放2个正方体和3个圆柱体,两个天平都平衡,则12个球体的质量等于( )个正方体的质量.
如图所示,第一个天平的两侧分别放2个球体和5个圆柱体,第二个天平的两侧分别放2个正方体和3个圆柱体,两个天平都平衡,则12个球体的质量等于( )个正方体的质量.