题目内容
12．
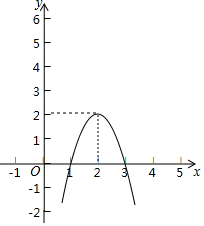如图，二次函数y=-2（x-2）2+2的图象．（1）由图象直接写出y随x的增大而减小的自变量x的取值范围；直接写出抛物线与x轴的交点坐标．
（2）将该图象绕顶点旋转180度后，再沿着x轴向左平移3个单位，沿着y轴向下平移3个单位，画出运动后的图象，并写出最后的解析式．
分析 （1）根据函数图象写出对称轴右边部分的x的取值范围即可，根据函数图象与x轴交点写出坐标即可；
（2）根据旋转变换只改变图形的位置不改变图形的形状与大小可知二次项系数的绝对值不变，再根据向左平移横坐标减，向下平移纵坐标减求出平移后的抛物线顶点坐标，然后作出函数图象并写出解析式即可．
解答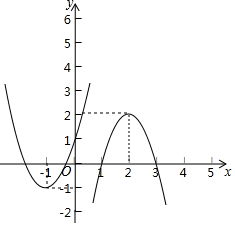 
解：（1）由图可知，x＞2时，y随x的增大而减小，
抛物线与x轴的交点坐标为（1，0），（3，0）；
（2）运动后图象如图所示，
二次函数y=-2（x-2）2+2的顶点坐标为（2，2），
∵绕顶点旋转180度后，再沿着x轴向左平移3个单位，沿着y轴向下平移3个单位，
2-3=-1，
2-3=-1，
∴平移后的函数图象顶点坐标为（-1，-1），
∴函数解析式为y=2（x+1）2+1．
点评 本题考查了抛物线与x轴的交点问题，二次函数图象与几何变换，平移后的函数解析式利用顶点的变化求解更简便．
练习册系列答案
阅读快车系列答案
相关题目
3．下列算式中，错误的是（ ）
| A． | a（a+b）+b（a+b）=a2+2ab+b2 | B． | x（x-y）+y（x-y）=x2-y2 | ||
| C． | a（a2-ab+b2）+b（a2-ab+b2）=a3+b3 | D． | x（x-y）-y（x-y）=y2-x2 |
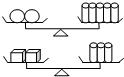如图所示，第一个天平的两侧分别放2个球体和5个圆柱体，第二个天平的两侧分别放2个正方体和3个圆柱体，两个天平都平衡，则12个球体的质量等于（ ）个正方体的质量．
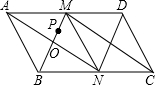如图所示，在平行四边形ABCD中，M，N分别是AD，BC的中点，∠BMC=90°，连接AN，DN，AN与BM交于点O．
甲、乙两车分别从A，B两地同时相向匀速行驶，当乙车到达A地后，继续保持原速向远离B的方向行驶，而甲车到达B地后立即掉头，并保持原速与乙车同向行驶，经过15小时后两车同时到达距A地300千米的C地（中途休息时间忽略不计）．设两车行驶的时间为x（小时），两车之间的距离为y（千米），y与x之间的函数关系如图所示，则当甲车到达B地时，乙车距A地100千米．