题目内容
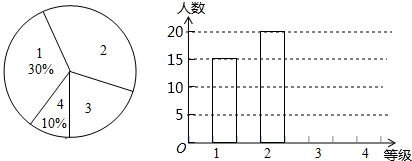 新的交通法规实施后,驾校的考试规则也发生了变化,考试共设四个科目:科目1、科目2、科目3和科目4,以下简记为:1、2、3、4.四个科目考试在同一地点进行,但每个学员每次只能够参加一个科目考试.在某次考试中,对该考点各科目考试人数进行了调查统计,并根据调查结果绘制成如图所示的条形统计图和扇形统计图(未完成),请结合图中所给信息解答下列问题:
新的交通法规实施后,驾校的考试规则也发生了变化,考试共设四个科目:科目1、科目2、科目3和科目4,以下简记为:1、2、3、4.四个科目考试在同一地点进行,但每个学员每次只能够参加一个科目考试.在某次考试中,对该考点各科目考试人数进行了调查统计,并根据调查结果绘制成如图所示的条形统计图和扇形统计图(未完成),请结合图中所给信息解答下列问题:(1)本次被调查的学员共有
(2)该考点参加“科目4”考试的学员里有3位是教师,某新闻部门准备在该考点参加“科目4”考试的学员中随机选出2位,调查他们对新规的了解情况,请你用列表法或画树状图的方法求出所选两位学员恰好都是教师的概率.
考点:扇形统计图,列表法与树状图法
专题:
分析:(1)根据选择科目1的人数是15,所占的百分比是30%即可求得总人数,然后根据百分比的意义求得科目4的人数,进而求得科目3的人数,补全直方图;
(2)利用树状图法即可列举出出现的所有情况,然后利用概率公式即可求解.
(2)利用树状图法即可列举出出现的所有情况,然后利用概率公式即可求解.
解答:解:(1)调查的总人数是:15÷30%=50(人),
参加科目4的人数是:50×10%=5(人),
则被调查者中参加“科目3”测试的有:50-15-20-5=10(人).
故答案是:50,10.
 ;
;
(2)三位教师用A1、A2、A3表示,另两位学员用B、C表示.

则共有20种情况,所选两位学员恰好都是教师的有6种情况,则概率是:
=
.
参加科目4的人数是:50×10%=5(人),
则被调查者中参加“科目3”测试的有:50-15-20-5=10(人).
故答案是:50,10.
 ;
;(2)三位教师用A1、A2、A3表示,另两位学员用B、C表示.

则共有20种情况,所选两位学员恰好都是教师的有6种情况,则概率是:
| 6 |
| 20 |
| 3 |
| 10 |
点评:本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.

练习册系列答案
相关题目
化简|3-π|的结果为( )
| A、3-π | B、-3-π |
| C、3+π | D、π-3 |
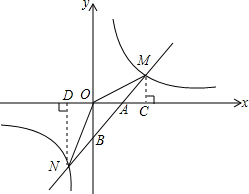 如图,已知反比例函数y=
如图,已知反比例函数y=

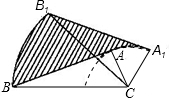 如图,在Rt△ABC中,∠BAC=90°,AB=6cm,AC=3cm,将△ABC绕顶点C按顺时针方向旋转45°至△A1B1C1的位置,则线段AB扫过区域(图中的阴影部分)的面积为
如图,在Rt△ABC中,∠BAC=90°,AB=6cm,AC=3cm,将△ABC绕顶点C按顺时针方向旋转45°至△A1B1C1的位置,则线段AB扫过区域(图中的阴影部分)的面积为 如图,延长线AB到C使BC=
如图,延长线AB到C使BC=