题目内容
如图1,在Rt△ABC中,∠ACB=90°,AC=BC,CD⊥AB于点D
(1)把Rt△DBC绕点D顺时针旋转45°,点C的对称点为E,点B的对称点为F,请画出△EDF,连接AE,BE,并求∠AEB的度数.
(2)如图2,把Rt△DBC绕点D顺时针旋转α度(0<α<90°),点C的对称点为E,点B的对称点为F,连接CE,则线段AE,BE与CE之间有何确定的数量关系?写出关系式并加以证明.

(1)把Rt△DBC绕点D顺时针旋转45°,点C的对称点为E,点B的对称点为F,请画出△EDF,连接AE,BE,并求∠AEB的度数.
(2)如图2,把Rt△DBC绕点D顺时针旋转α度(0<α<90°),点C的对称点为E,点B的对称点为F,连接CE,则线段AE,BE与CE之间有何确定的数量关系?写出关系式并加以证明.

考点:旋转的性质
专题:
分析:(1)根据旋转的定义画图,如图1,根据等腰直角三角形的性质得AD=BD=CD,再根据等腰三角形的性质得∠DEA=∠DAE,∠DEB=∠DBE,然后利用三角形内角和定理可计算出∠DEA+∠DEB=90°,即∠AEB的度数为90°;
(2)作CM⊥CE交AE于M,如图2,根据旋转的性质得∠CDE=α°,DE=DC=DA,利用互余得∠BDE=90-α,根据三角形内角和定理得∠DEC=90°-
α,则根据三角形外角性质可计算出∠DEA=
∠BDE=45°-
α,所以∠AEC=∠DEC-∠DEA=45°,由此可判断△CEM为等腰直角三角形,得到CE=CM,EM=
EC,然后根据旋转的定义,把△CAM绕点C逆时针旋转90°可得到△CBE,则AM=BE,所以AE=AM+EM=BE+
CE.
(2)作CM⊥CE交AE于M,如图2,根据旋转的性质得∠CDE=α°,DE=DC=DA,利用互余得∠BDE=90-α,根据三角形内角和定理得∠DEC=90°-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
解答: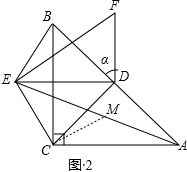 解:(1)
解:(1)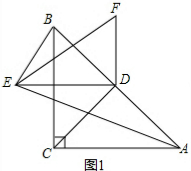 如图1,
如图1,
∵∠ACB=90°,AC=BC,CD⊥AB,
∴AD=BD=CD,
∴∠DEA=∠DAE,∠DEB=∠DBE,
∴∠DEA+∠DEB=
(∠DEA+∠DAE+∠DEB+∠DBE)=
×180°=90°,
即∠AEB的度数为90°;
(2)线段AE,BE与CE之间的数量关系为AE=BE+
CE.理由如下:
作CM⊥CE交AE于M,如图2,
∵Rt△DBC绕点D顺时针旋转α度(0<α<90°),点C的对称点为E,点B的对称点为F,
∴∠CDE=α°,DE=DC=DA,
∴∠BDE=90-α,∠DEC=
(180°-∠EDC)=90°-
α,
而∠BDE=∠DEA+∠DAE,
∴∠DEA=
∠BDE=45°-
α
∴∠AEC=∠DEC-∠DEA=90°-
α-(45°-
α)=45°,
∵CM⊥EC,
∴∠ECM=90°,
∴△CEM为等腰直角三角形,
∴CE=CM,EM=
EC,
∵∠ACB=∠MCE=90°,CA=CB,CM=CE,
∴△CAM绕点C逆时针旋转90°可得到△CBE,
∴AM=BE,
∴AE=AM+EM=BE+
CE.
 解:(1)
解:(1) 如图1,
如图1,∵∠ACB=90°,AC=BC,CD⊥AB,
∴AD=BD=CD,
∴∠DEA=∠DAE,∠DEB=∠DBE,
∴∠DEA+∠DEB=
| 1 |
| 2 |
| 1 |
| 2 |
即∠AEB的度数为90°;
(2)线段AE,BE与CE之间的数量关系为AE=BE+
| 2 |
作CM⊥CE交AE于M,如图2,
∵Rt△DBC绕点D顺时针旋转α度(0<α<90°),点C的对称点为E,点B的对称点为F,
∴∠CDE=α°,DE=DC=DA,
∴∠BDE=90-α,∠DEC=
| 1 |
| 2 |
| 1 |
| 2 |
而∠BDE=∠DEA+∠DAE,
∴∠DEA=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠AEC=∠DEC-∠DEA=90°-
| 1 |
| 2 |
| 1 |
| 2 |
∵CM⊥EC,
∴∠ECM=90°,
∴△CEM为等腰直角三角形,
∴CE=CM,EM=
| 2 |
∵∠ACB=∠MCE=90°,CA=CB,CM=CE,
∴△CAM绕点C逆时针旋转90°可得到△CBE,
∴AM=BE,
∴AE=AM+EM=BE+
| 2 |
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等腰直角三角形的性质和等腰三角形的性质.

练习册系列答案
相关题目
方程x2-x-1=
的解的情况是( )
| 1 |
| x-1 |
| A、仅有一正根 |
| B、仅有一负根 |
| C、一正根一负根 |
| D、两个不相等的实数根 |
石家庄市10月份某七天的最低气温(单位:℃)分别为14,10,11,14,14,13,8,则这组数据中的中位数和众数分别是( )
| A、13,13 |
| B、14,14 |
| C、13,14 |
| D、14,13 |
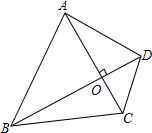 如图,四边形ABCD的两条对角线AC、BD相互垂直,垂足为O,且AC+BD=10,设AC长为x,四边形ABCD的面积为S.
如图,四边形ABCD的两条对角线AC、BD相互垂直,垂足为O,且AC+BD=10,设AC长为x,四边形ABCD的面积为S. 如图,AC⊥CB,垂足为C点,AC=CB=8cm,点Q是AC的中点,动点P由B点出发,沿射线BC方向匀速移动.点P的运动速度为2cm/s.设动点P运动的时间为ts.为方便说明,我们分别记三角形ABC面积为S,三角形PCQ的面积为S1,三角形PAQ的面积为S2,三角形ABP的面积为S3.
如图,AC⊥CB,垂足为C点,AC=CB=8cm,点Q是AC的中点,动点P由B点出发,沿射线BC方向匀速移动.点P的运动速度为2cm/s.设动点P运动的时间为ts.为方便说明,我们分别记三角形ABC面积为S,三角形PCQ的面积为S1,三角形PAQ的面积为S2,三角形ABP的面积为S3.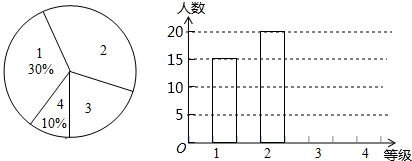 新的交通法规实施后,驾校的考试规则也发生了变化,考试共设四个科目:科目1、科目2、科目3和科目4,以下简记为:1、2、3、4.四个科目考试在同一地点进行,但每个学员每次只能够参加一个科目考试.在某次考试中,对该考点各科目考试人数进行了调查统计,并根据调查结果绘制成如图所示的条形统计图和扇形统计图(未完成),请结合图中所给信息解答下列问题:
新的交通法规实施后,驾校的考试规则也发生了变化,考试共设四个科目:科目1、科目2、科目3和科目4,以下简记为:1、2、3、4.四个科目考试在同一地点进行,但每个学员每次只能够参加一个科目考试.在某次考试中,对该考点各科目考试人数进行了调查统计,并根据调查结果绘制成如图所示的条形统计图和扇形统计图(未完成),请结合图中所给信息解答下列问题: