题目内容
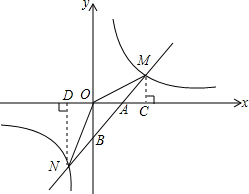 如图,已知反比例函数y=
如图,已知反比例函数y=| k |
| x |
(1)求这两个函数的解析式;
(2)求△MON的面积;
(3)根据图象写出使反比例函数的值大于一次函数的值的x的取值范围.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)先把N点坐标代入y=
,求出k得反比例函数解析式为y=
,再利用反比例函数解析式确定M点的坐标为(2,2),然后利用待定系数法求一次函数解析式;
(2)先求出A点的坐标,再根据三角形的面积公式求出三角形AOM和三角形AON的面积,相加即可得出答案;
(3)观察函数图象得到当x<-1或0<x<2时,反比例函数图象都在一次函数图象上方,即反比例函数的值大于一次函数的值.
| k |
| x |
| 4 |
| x |
(2)先求出A点的坐标,再根据三角形的面积公式求出三角形AOM和三角形AON的面积,相加即可得出答案;
(3)观察函数图象得到当x<-1或0<x<2时,反比例函数图象都在一次函数图象上方,即反比例函数的值大于一次函数的值.
解答:解:(1)把N(-1,-4)代入y=
,
得k=-1×(-4)=4,
所以反比例函数解析式为y=
;
把M(2,m)代入y=
,
得2m=4,解得m=2,
则M点的坐标为(2,2).
把M(2,2),N(-1,-4)代入y=ax+b,
得
,解得
,
 所以一次函数解析式为y=2x-2;
所以一次函数解析式为y=2x-2;
(2)如图,作MC⊥x轴于点C,作ND⊥x轴于点D.
∵y=2x-2,
∴y=0时,x=1,
∴A(1,0),即OA=1,
∴S△MON=S△MOA+S△NOA=
OA•MC+
OA•ND=
×1×2+
×1×4=3;
(3)由图象可知,当x<-1或0<x<2时,反比例函数的值大于一次函数的值.
| k |
| x |
得k=-1×(-4)=4,
所以反比例函数解析式为y=
| 4 |
| x |
把M(2,m)代入y=
| 4 |
| x |
得2m=4,解得m=2,
则M点的坐标为(2,2).
把M(2,2),N(-1,-4)代入y=ax+b,
得
|
|
 所以一次函数解析式为y=2x-2;
所以一次函数解析式为y=2x-2;(2)如图,作MC⊥x轴于点C,作ND⊥x轴于点D.
∵y=2x-2,
∴y=0时,x=1,
∴A(1,0),即OA=1,
∴S△MON=S△MOA+S△NOA=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(3)由图象可知,当x<-1或0<x<2时,反比例函数的值大于一次函数的值.
点评:本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数图象的交点坐标满足两函数解析式.也考查了待定系数法求函数解析式,三角形的面积以及观察函数图象的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
嘉绍跨海大桥在2013年7月19日建成通车,此项目总投资约139亿元,139亿元用科学记数法表示为( )
| A、1.39×1010元 |
| B、1.39×1011元 |
| C、0.139×1012元 |
| D、13.9×109元 |
方程x2-x-1=
的解的情况是( )
| 1 |
| x-1 |
| A、仅有一正根 |
| B、仅有一负根 |
| C、一正根一负根 |
| D、两个不相等的实数根 |
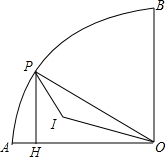 如图,半径为2cm,圆心角为90°的扇形OAB的弧AB上有一动点P.过P作PH⊥OA于H,设I为△OPH的内心,
如图,半径为2cm,圆心角为90°的扇形OAB的弧AB上有一动点P.过P作PH⊥OA于H,设I为△OPH的内心,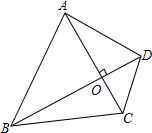 如图,四边形ABCD的两条对角线AC、BD相互垂直,垂足为O,且AC+BD=10,设AC长为x,四边形ABCD的面积为S.
如图,四边形ABCD的两条对角线AC、BD相互垂直,垂足为O,且AC+BD=10,设AC长为x,四边形ABCD的面积为S.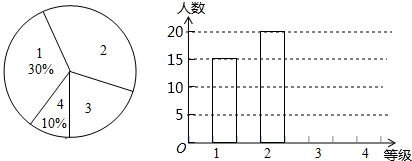 新的交通法规实施后,驾校的考试规则也发生了变化,考试共设四个科目:科目1、科目2、科目3和科目4,以下简记为:1、2、3、4.四个科目考试在同一地点进行,但每个学员每次只能够参加一个科目考试.在某次考试中,对该考点各科目考试人数进行了调查统计,并根据调查结果绘制成如图所示的条形统计图和扇形统计图(未完成),请结合图中所给信息解答下列问题:
新的交通法规实施后,驾校的考试规则也发生了变化,考试共设四个科目:科目1、科目2、科目3和科目4,以下简记为:1、2、3、4.四个科目考试在同一地点进行,但每个学员每次只能够参加一个科目考试.在某次考试中,对该考点各科目考试人数进行了调查统计,并根据调查结果绘制成如图所示的条形统计图和扇形统计图(未完成),请结合图中所给信息解答下列问题: