题目内容
13. 如图,AD∥BC,∠A=104°,∠D=126°,BE、CE分别是∠ABC和∠BCD的角平分线,则∠BEC的度数为115°.
如图,AD∥BC,∠A=104°,∠D=126°,BE、CE分别是∠ABC和∠BCD的角平分线,则∠BEC的度数为115°.
分析 根据平行线的性质得出∠A+∠ABC=180°,∠D+∠DCB=180°,求出∠ABC=76°,∠DCB=54°,根据角平分线的定义求出∠EBC和∠ECB,根据三角形内角和定理求出即可.
解答 解:∵AD∥BC,
∴∠A+∠ABC=180°,∠D+∠DCB=180°,
∵∠A=104°,∠D=126°,
∴∠ABC=76°,∠DCB=54°,
∵BE、CE分别是∠ABC和∠BCD的角平分线,
∴∠EBC=$\frac{1}{2}$∠ABC=38°,∠ECB=$\frac{1}{2}$∠DCB=27°,
∴∠BEC=180°-∠EBC-∠ECB=115°,
故答案为:115.
点评 本题考查了平行线的性质,三角形的内角和定理,角平分线定义的应用,能求出∠ABC和∠DCB的度数是解此题的关键,注意:两直线平行,同旁内角互补.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.下列五种图形中,正方体的截平面不可能出现的图形有( )
(1)钝角三角形;(2)直角三角形;(3)菱形;(4)正五边形;(5)正六边形.
(1)钝角三角形;(2)直角三角形;(3)菱形;(4)正五边形;(5)正六边形.
| A. | (1)(2)(5) | B. | (1)(2)(4) | C. | (2)(3)(4) | D. | (3)(4)(5) |
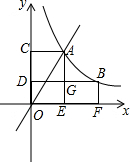 如图,直线y=2x与反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象交于点A(1,a),点B是反比例函数图象上的任意一点(不与A点重合).
如图,直线y=2x与反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象交于点A(1,a),点B是反比例函数图象上的任意一点(不与A点重合).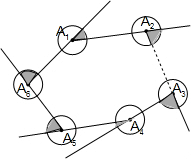 如图所示,分别以n边形顶角顶点为圆心,以2cm长为半径画圆,则圆中阴影部分面积之和为4πcm2.
如图所示,分别以n边形顶角顶点为圆心,以2cm长为半径画圆,则圆中阴影部分面积之和为4πcm2.