题目内容
8.解下列分式方程:①$\frac{7}{x+2}$+2=$\frac{1-3x}{x+2}$
②$\frac{3}{x-1}$-$\frac{x+3}{{{x^2}-1}}$=0.
分析 两分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:①去分母得:7+2(x+2)=1-3x,
去括号得:7+2x+4=1-3x,
移项合并得:5x=-10,
解得:x=-2,
经检验x=-2是增根,分式方程无解;
②去分母得:3(x+1)-x-3=0,
去括号得:3x+3-x-3=0,
移项合并得:2x=0,
解得:x=0,
经检验x=0是分式方程的解.
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
相关题目
18.方程$\sqrt{x+1}$=5-x的解是( )
| A. | x=3 | B. | x=8 | C. | x1=3,x2=8 | D. | x1=3,x2=-8 |
18.在$\sqrt{6}$,0,-2,3这四个数中,最大的数是( )
| A. | $\sqrt{6}$ | B. | 0 | C. | -2 | D. | 3 |
 如图,AD∥BC,∠A=104°,∠D=126°,BE、CE分别是∠ABC和∠BCD的角平分线,则∠BEC的度数为115°.
如图,AD∥BC,∠A=104°,∠D=126°,BE、CE分别是∠ABC和∠BCD的角平分线,则∠BEC的度数为115°.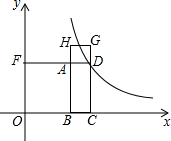 已知点D是反比例函数上一点,矩形ABCD的周长是16,正方形ABOF和正方形ADGH的面积之和为50,则反比例函数的解析式是$y=\frac{8}{x}$或$y=\frac{56}{x}$.
已知点D是反比例函数上一点,矩形ABCD的周长是16,正方形ABOF和正方形ADGH的面积之和为50,则反比例函数的解析式是$y=\frac{8}{x}$或$y=\frac{56}{x}$.