题目内容
8.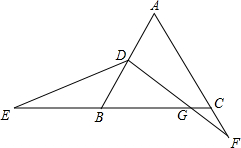 如图,在等边△ABC中,点D为AB边中点,点E在CB的延长线上,点F在AC的延长线上,DF交BC于点G且∠EDF=120°.若CE=8,CF=2,则CG=1.
如图,在等边△ABC中,点D为AB边中点,点E在CB的延长线上,点F在AC的延长线上,DF交BC于点G且∠EDF=120°.若CE=8,CF=2,则CG=1.
分析 作DH∥BC交AC于H,如图,根据等边三角形的性质得AB=BC=AC,∠ABC=∠ACB=60°,由于点D为AB边中点,则BD=DH=CH,利用DH∥BC得到∠BDH=∠CHD=120°,而∠EDF=120°,则∠EDB=∠HDF,于是可根据“ASA”证明△BDE≌△HDF得到BE=FH,则BE+BC=2+$\frac{1}{2}$BC+BC=8,得到BC=8,所以DH=CH=2,然后证明△FCG∽△FHD,利用相似比可计算出CG.
解答 解:作DH∥BC交AC于H,如图,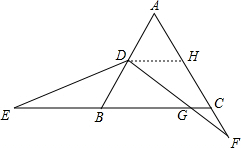
∵△ABC为等边三角形,
∴AB=BC=AC,∠ABC=∠ACB=60°,
∵点D为AB边中点,
∴BD=DH=CH,
∵DH∥BC,
∴∠BDH=∠CHD=120°,
而∠EDF=120°,
∴∠EDB=∠HDF,
在△BDE和△HDF中
$\left\{\begin{array}{l}{∠EDB=∠FDH}\\{BD=DH}\\{∠DBE=∠DHF}\end{array}\right.$,
∴△BDE≌△HDF,
∴BE=FH,
∵BE+BC=CE=8,
∴CF+$\frac{1}{2}$BC+BC=8,即2+$\frac{3}{2}$BC=8,
∴BC=4,
∴DH=CH=2,
∵CG∥DH,
∴△FCG∽△FHD,
∴$\frac{CG}{DH}$=$\frac{CF}{FH}$,即$\frac{CG}{2}$=$\frac{2}{2+2}$,
∴CG=1.
故答案为1.
点评 本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形.也考查了全等三角形的判定与性质和等边三角形的判定与性质.

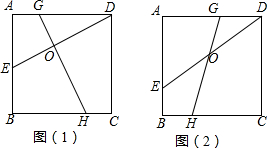
 已知:矩形ABCD中,对角线AC与BD交于点O,∠BOC=120°,AC=4cm,求矩形ABCD的周长.
已知:矩形ABCD中,对角线AC与BD交于点O,∠BOC=120°,AC=4cm,求矩形ABCD的周长. 如图,小明把一块含有60°角的直角三角尺的两个顶点放在直尺的对边上,并测得∠1=20°,则∠2的度数是40°.
如图,小明把一块含有60°角的直角三角尺的两个顶点放在直尺的对边上,并测得∠1=20°,则∠2的度数是40°.