题目内容
18．解不等式（或不等式组）：（1）解不等式$\frac{x+1}{3}＜\frac{3x}{2}$
（2）解不等式组$\left\{\begin{array}{l}x-3（{x-2}）≥0\\ \frac{2x-1}{3}＞\frac{1}{2}x-1\end{array}\right.$．
分析 （1）利用不等式的性质求得不等式的解集即可；
（2）分别求出不等式组中两不等式的解集，利用不等式组取解集的方法得出原不等式的解集．
解答 解：（1）$\frac{x+1}{3}＜\frac{3x}{2}$
2（x+1）＜9x
-7x＜-2
x＞$\frac{2}{7}$；
（2）$\left\{\begin{array}{l}{x-3（x-2）≥0①}\\{\frac{2x-1}{3}＞\frac{1}{2}x-1②}\end{array}\right.$
解不等式①得x≤3，
解不等式②得x＞-4，
所以不等式组的解集为-4＜x≤3．
点评 此题考查了一元一次不等式于一元一次不等式组的解法，不等式组取解集的方法为：“同大取大”；“同小取小”；“大大小小无解”；“大小小大取中间”．
练习册系列答案
相关题目
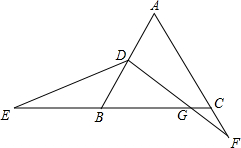如图，在等边△ABC中，点D为AB边中点，点E在CB的延长线上，点F在AC的延长线上，DF交BC于点G且∠EDF=120°．若CE=8，CF=2，则CG=1．