题目内容
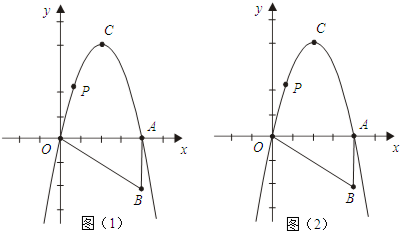
20.如图,Rt△OAB中,∠OAB=90°,直角边OA与x轴重合,OA=4,AB=2,现在把Rt△OAB绕点O逆时针旋转90°,点B旋转到点C的位置,一条抛物线正好经过点O,C,A三点.(1)求该抛物线的解析式;
(2)在x轴上方的抛物线上有一动点P,过点P作x轴的平行线交抛物线于点G;分别过点P,点G作x轴的垂线,交x轴于E,F两点.
问:四边形PEFG的周长是否有最大值?若有,求出最值,并写出解答过程;若没有,请说明理由.
分析 (1)根据旋转的性质可求出C的坐标和A的坐标,又因为抛物线经过原点,故设y=ax2+bx把(2,4),(4,0)代入,求出a和b的值即可求出该抛物线的解析式;
(2)四边形PEFM的周长有最大值,设点P的坐标为P(a,-a2+4a)则由抛物线的对称性知OE=AF,所以EF=PG=4-2a,PE=MF=-a2+4a,则矩形PEFG的周长L=2[4-2a+(-a2+4a)]=-2(a-1)2+10,利用函数的性质即可求出四边形PEFM的周长的最大值.
解答 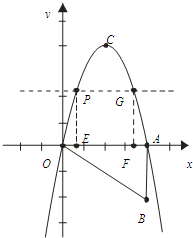 解:(1)∵OA=4,AB=2,△AOB绕点O逆时针旋转90°,点B旋转到点C的位置,
解:(1)∵OA=4,AB=2,△AOB绕点O逆时针旋转90°,点B旋转到点C的位置,
∴点C的坐标为(2,4).
又∵点A的坐标为(4,0),抛物线经过原点,故设y=ax2+bx(a≠0),把(2,4),(4,0)代入,得
$\left\{\begin{array}{l}{0=16a+4b}\\{4=4a+2b}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-1}\\{b=4}\end{array}\right.$.
所以抛物线的解析式为y=-x2+4x;
(2)有最大值.
理由如下:设点P的坐标为P(a,-a2+4a),PE=GF=-a2+4a,
则由抛物线的对称性知OE=AF,所以EF=PG=4-2a,
则矩形PEFG的周长L=2[4-2a+(-a2+4a)]=-2(a-1)2+10,
所以当a=1时,矩形PEFM的周长有最大值,Lmax=10.
点评 本题考查了旋转的性质、利用待定系数法求二次函数的解析式、二次函数的最大值问题和函数图象的交点问题,题目的综合性很强,对学生的综合解题能力要求很高.

练习册系列答案
相关题目
9.在实数$\root{3}{9}$,3.1415926,$\frac{22}{7}$,-8,$\sqrt{8}$,$\sqrt{16}$,1.010010001…,$\frac{π}{3}$中无理数有( )
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
10.点A关于x轴对称的点为A′(3,-2),则点A的关于原点的对称点坐标是( )
| A. | (3,2) | B. | (-3,2) | C. | (-3,-2) | D. | (-2,3) |
5.为配合中国倡导的“一带一路”建设的愿景,成立的亚洲基础设施投资银行(亚投行)截止 3月31日关上了申请大门,共有46个国家和地区成为创始成员国,中期计划投资总额即达4700亿美元.其中4700亿美元用科学记数法表示为( )
| A. | 47×1010 | B. | 4700×108 | C. | 4.7×1011 | D. | 4.7×1010 |
12.数据2,4,8,2的中位数和众数是( )
| A. | 3和2 | B. | 2和3 | C. | 6和2 | D. | 2和6 |
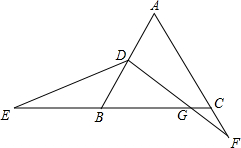 如图,在等边△ABC中,点D为AB边中点,点E在CB的延长线上,点F在AC的延长线上,DF交BC于点G且∠EDF=120°.若CE=8,CF=2,则CG=1.
如图,在等边△ABC中,点D为AB边中点,点E在CB的延长线上,点F在AC的延长线上,DF交BC于点G且∠EDF=120°.若CE=8,CF=2,则CG=1.