题目内容
5.先化简,再求值:$\frac{{{x^2}-1}}{x}÷\frac{x+1}{x}+1$,其中$x=\frac{1}{tan60°}$.分析 先化除法为乘法,对所求的代数式进行化简,然后代入求值.
解答 解:原式=$\frac{(x+1)(x-1)}{x}$×$\frac{x}{x+1}$+1,
=x-1+1,
=x.
把$x=\frac{1}{tan60°}$=$\frac{\sqrt{3}}{3}$代入,得
原式=x=$\frac{{\sqrt{3}}}{3}$.
点评 本题考查了分式的化简求值,特殊角的三角函数值.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.

练习册系列答案
相关题目
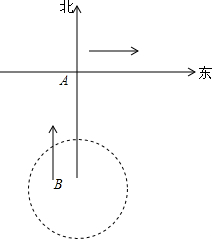 一艘轮船以20海里/时的速度由西向东航行,在途中接到台风警报,台风中心正以40海里/时的速度由南向北移动,距台风中心20海里的圆形区域(包括边界)都属于台风区域,当轮船到A处时测得台风中心移到位于点A正南方的B处,且AB=100海里.若这艘轮船自A处按原速度继续航行,在途中是否会遇到台风?若会,则求出轮船最初遇到台风的时间;若不会,请说明理由.
一艘轮船以20海里/时的速度由西向东航行,在途中接到台风警报,台风中心正以40海里/时的速度由南向北移动,距台风中心20海里的圆形区域(包括边界)都属于台风区域,当轮船到A处时测得台风中心移到位于点A正南方的B处,且AB=100海里.若这艘轮船自A处按原速度继续航行,在途中是否会遇到台风?若会,则求出轮船最初遇到台风的时间;若不会,请说明理由.